题目内容
8.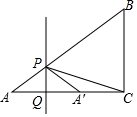 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,点P为线段AB上一动点,直线PQ⊥AC于点Q,点A关于PQ的对称点A′落在直线AC上,若△A′PC为等腰三角形,则AP的长为$\frac{20}{13}$.
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,点P为线段AB上一动点,直线PQ⊥AC于点Q,点A关于PQ的对称点A′落在直线AC上,若△A′PC为等腰三角形,则AP的长为$\frac{20}{13}$.
分析 由勾股定理求出AB,再根据轴对称的性质解答即可.
解答 解:∵Rt△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=$\sqrt{{4}^{2}+{3}^{2}}=5$,
∵直线PQ⊥AC于点Q,点A关于PQ的对称点A′落在直线AC上,
∴PA=PA',AQ=A'Q,
∵△A′PC为等腰三角形,
∴PA'=A'C,
∵PQ⊥AC,∠ACB=90°,
∴设PA=5x,AQ=QA'=4x,A'C=PA'=PA=5x,
∴4x+4x+5x=4,
解得:x=$\frac{4}{13}$,
∴PA=$5×\frac{4}{13}=\frac{20}{13}$.
故答案为:$\frac{20}{13}$
点评 本题考查了轴对称的性质、等腰三角形的性质;关键是由勾股定理求出AB进行解答.

练习册系列答案
相关题目
13.已知$\frac{3}{x}$=$\frac{5}{y}$,则$\frac{{x}^{2}-xy+2{y}^{2}}{{x}^{2}-2xy}$的值为( )
| A. | -$\frac{44}{21}$ | B. | $\frac{8}{5}$ | C. | $\frac{44}{21}$ | D. | -$\frac{8}{5}$ |
 如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M.
如图,正方形ABCD的对角线AC、BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M.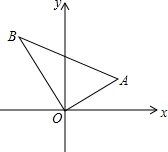 如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积.
如图,Rt△ABO的顶点在原点,OA=12,AB=20,∠AOx=30°,求A,B两点的坐标,并求△AOB的面积. 如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F.求证:AF•AB+CD•CB=AC2.
如图,在△ABC中,AD为内角平分线,∠ADC=60°,点E在AD上,满足DE=DB,射线CE交AB于点F.求证:AF•AB+CD•CB=AC2. 已知?ABCD,连结对角线BD,E、F是边BC的三等分点,连结AE、AF,与BD分别交于点G、H,则BG:GH:HD的值为5:3:12.
已知?ABCD,连结对角线BD,E、F是边BC的三等分点,连结AE、AF,与BD分别交于点G、H,则BG:GH:HD的值为5:3:12.