题目内容
17.(1)解方程:①x2-6x-4=0
②x2-12x+27=0
(2)直接写出方程(x2-6x-4)(x2-12x+27)=0的解为x1=3+$\sqrt{13}$,x2=3-$\sqrt{13}$,x3=3,x4=9.
分析 (1)①按照步骤:移项,把常数项移到右边,左右两边加上一次项系数一半的平方,写成完全平方式,直接开方;
②将方程的左边因式分解,将一元二次方程转化为两个一元一次方程,即可解决问题;
(2)由(x2-6x-4)(x2-12x+27)=0,得出x2-6x-4=0,x2-12x+27=0把两个方程的解合并在一起即可.
解答 解:(1)①x2-6x-4=0
x2-6x=4,
x2-6x+9=4+9,
(x-3)2=13,
x-3=±$\sqrt{13}$,
∴x1=3+$\sqrt{13}$,x2=3-$\sqrt{13}$;
②x2-12x+27=0,
(x-3)(x-9)=0,
x-3=0,x-9=0,
解得:x1=3,x2=9;
方程(x2-6x-4)(x2-12x+27)=0的解为x1=3+$\sqrt{13}$,x2=3-$\sqrt{13}$,x3=3,x4=9.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
9.下列命题中,假命题是( )
| A. | 四个内角都相等的四边形是矩形 | |
| B. | 四条边都相等的平行四边形是正方形 | |
| C. | 既是菱形又是矩形的四边形是正方形 | |
| D. | 对角线互相垂直的平行四边形是菱形 |
 如图,△ABC中,∠C=90°,∠A=30°,BC=1.5cm,则AB的长是3cm.
如图,△ABC中,∠C=90°,∠A=30°,BC=1.5cm,则AB的长是3cm.
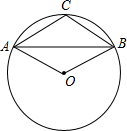 如图,已知A,B,C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是$\sqrt{3}$.
如图,已知A,B,C是半径为1的⊙O上三点,且四边形AOBC是平行四边形,则弦AB的长是$\sqrt{3}$.