题目内容
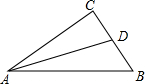 如图,在△ABC中,∠C=90°,AC=4,BC=3,AD平分∠CAB,交BC于D,点P是边AB上的动点(点P与A,B不重合),设PB=x,△DPB的面积为y.
如图,在△ABC中,∠C=90°,AC=4,BC=3,AD平分∠CAB,交BC于D,点P是边AB上的动点(点P与A,B不重合),设PB=x,△DPB的面积为y.(1)求CD的长;
(2)求y关于x的函数关系式,写出自变量x的范围.
考点:角平分线的性质,函数关系式,勾股定理
专题:
分析:(1)由勾股定理求出AB的长,过点D作DE⊥AB于点E,根据角平分线的性质可知CD=DE,再由三角形的面积公式可得出CD的长;
(2)根据三角形的面积公式即可得出结论.
(2)根据三角形的面积公式即可得出结论.
解答: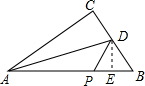 解:(1)∵在△ABC中,∠C=90°,AC=4,BC=3,
解:(1)∵在△ABC中,∠C=90°,AC=4,BC=3,
∴AB=
=5.
过点D作DE⊥AB于点E,
∵AD平分∠CAB,
∴CD=DE.
∵S△ABC=S△ACD+S△ABD,即
×3×4=
×4CD+
×5CD,解得CD=
;
(2)由(1)知,DE=
,
∵PB=x,△DPB的面积为y,
∴y=
PB•DE=
x×
=
x(0<x≤5).
 解:(1)∵在△ABC中,∠C=90°,AC=4,BC=3,
解:(1)∵在△ABC中,∠C=90°,AC=4,BC=3,∴AB=
| 32+42 |
过点D作DE⊥AB于点E,
∵AD平分∠CAB,
∴CD=DE.
∵S△ABC=S△ACD+S△ABD,即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
(2)由(1)知,DE=
| 4 |
| 3 |
∵PB=x,△DPB的面积为y,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
在同一平面内,两条直线可能的位置关系是( )
| A、平行 | B、相交 |
| C、相交或平行 | D、垂直 |
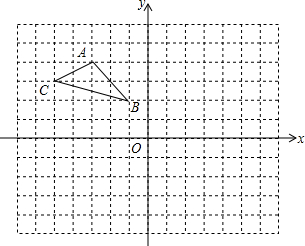 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-1,2),C(-5,3).
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-1,2),C(-5,3).
 如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为
如图,△ABC中,AB的中垂线DE交AB于E,交BC于D,若CB=10,AC=6,则△ACD的周长为 如图,在△ABC中,AB=AC=3cm,△BCN的周长是5cm,AB的垂直平分线交AC于点N,则BC=
如图,在△ABC中,AB=AC=3cm,△BCN的周长是5cm,AB的垂直平分线交AC于点N,则BC=