题目内容
 E点是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,延长CE交AD.BA的延长线于F,G.求证:BCDF是等腰梯形.
E点是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,延长CE交AD.BA的延长线于F,G.求证:BCDF是等腰梯形.考点:等腰梯形的判定
专题:证明题,几何综合题
分析:过点E作EH⊥CF交BC与H,判断出△CEH是等腰直角三角形,根据等腰直角三角形的性质可得CE=EH,再求出∠CED=∠HED=135°,然后利用“边角边”证明△CDE和△HDE全等,根据全等三角形对应边相等可得CD=DH,全等三角形对应角相等可得∠CDE=∠HDE,然后求出∠CBE=∠HDE,再利用“角角边”证明△BEH和△DHE全等,根据全等三角形对应边相等可得BH=DE,再求出BH=DF,然后根据一组对边平行且相等的四边形的平行四边形得到四边形BHDF是平行四边形,根据平行四边形对边相等可得BF=DH,从而得到BF=CD,再根据等腰梯形的定义证明即可.
解答:证明:如图,过点E作EH⊥CF交BC与H,
∵∠BCE=45°,
∴△CEH是等腰直角三角形,
∴CE=EH,
∵平行四边形ABCD对边AD∥BC,
∴∠DFE=∠BCE=45°,
∵DE⊥AD,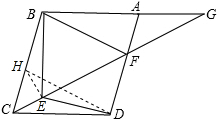
∴△DEF是等腰直角三角形,
∴DE=DF,∠DEF=45°,
∴∠CED=∠HED=135°,
在△CDE和△HDE中,
,
∴△CDE≌△HDE(SAS),
∴CD=DH,∠CDE=∠HDE,
∵∠CBE=∠CDE,
∴∠CBE=∠HDE,
在△BEH和△DHE中,
,
∴△BEH≌△DHE(AAS),
∴BH=DE,
又∵DE=DF,
∴BH=DF,
∵AD∥BC,
∴四边形BHDF是平行四边形,
∴BF=DH,
∴BF=CD,
∵AD∥BC,
∴BCDF是等腰梯形.
∵∠BCE=45°,
∴△CEH是等腰直角三角形,
∴CE=EH,
∵平行四边形ABCD对边AD∥BC,
∴∠DFE=∠BCE=45°,
∵DE⊥AD,

∴△DEF是等腰直角三角形,
∴DE=DF,∠DEF=45°,
∴∠CED=∠HED=135°,
在△CDE和△HDE中,
|
∴△CDE≌△HDE(SAS),
∴CD=DH,∠CDE=∠HDE,
∵∠CBE=∠CDE,
∴∠CBE=∠HDE,
在△BEH和△DHE中,
|
∴△BEH≌△DHE(AAS),
∴BH=DE,
又∵DE=DF,
∴BH=DF,
∵AD∥BC,
∴四边形BHDF是平行四边形,
∴BF=DH,
∴BF=CD,
∵AD∥BC,
∴BCDF是等腰梯形.
点评:本题考查了等腰梯形的判定,等腰直角三角形的判定与性质,平行四边形的判定与性质,全等三角形的判定与性质,综合题,难度较大,作辅助线构造出全等三角形是解题的关键,也是本题的难点.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
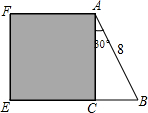 如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=8cm,以AC为边向形外作正方形ACEF,则正方形ACEF的面积为( )
如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=8cm,以AC为边向形外作正方形ACEF,则正方形ACEF的面积为( )| A、64cm2 |
| B、60cm2 |
| C、48cm2 |
| D、16cm2 |
 如图,在△ABC中,AB=AC=10,BC=16,点D在BA的延长线上,DE⊥BC,垂足为E,DE=CE,求DE的长.
如图,在△ABC中,AB=AC=10,BC=16,点D在BA的延长线上,DE⊥BC,垂足为E,DE=CE,求DE的长. 如图,在△ABC中,∠C=90°,D为BC边上一点,若∠ADC=45°,BD=2DC,求sin∠ABC和sin∠BAD的值.
如图,在△ABC中,∠C=90°,D为BC边上一点,若∠ADC=45°,BD=2DC,求sin∠ABC和sin∠BAD的值. 如图,已知三角形木块ABC,∠A=30°,∠B=90°,AC=10cm,一只蚂蚁在AC、AB间往返爬行.当蚂蚁从木块AC边的中点O出发,爬行到AB边上任意一点P后,又爬回到AC边上的任意一点Q后,再爬行到点B,在这一过程中这只蚂蚁爬行的最短距离为
如图,已知三角形木块ABC,∠A=30°,∠B=90°,AC=10cm,一只蚂蚁在AC、AB间往返爬行.当蚂蚁从木块AC边的中点O出发,爬行到AB边上任意一点P后,又爬回到AC边上的任意一点Q后,再爬行到点B,在这一过程中这只蚂蚁爬行的最短距离为