题目内容
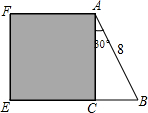 如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=8cm,以AC为边向形外作正方形ACEF,则正方形ACEF的面积为( )
如图,在△ABC中,∠ACB=90°,∠BAC=30°,AB=8cm,以AC为边向形外作正方形ACEF,则正方形ACEF的面积为( )| A、64cm2 |
| B、60cm2 |
| C、48cm2 |
| D、16cm2 |
考点:勾股定理,含30度角的直角三角形
专题:
分析:先根据直角三角形的性质求出BC的长,再由勾股定理求出AC的长,进而可得出结论.
解答:解:∵在△ABC中,∠ACB=90°,∠BAC=30°,AB=8cm,
∴BC=
AB=4(cm),
∴AC=
=
=4
(cm).
∵四边形ACEF是正方形,
∴S正方形ACEF=AC2=48(cm2).
故选C.
∴BC=
| 1 |
| 2 |
∴AC=
| AB2-BC2 |
| 82-42 |
| 3 |
∵四边形ACEF是正方形,
∴S正方形ACEF=AC2=48(cm2).
故选C.
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
 如图所示:∠AOB的内部有一点P,到顶点O的距离为5cm,M、N分别是射线OA、OB上的动点.若∠AOB=30°,则△PMN周长的最小值为
如图所示:∠AOB的内部有一点P,到顶点O的距离为5cm,M、N分别是射线OA、OB上的动点.若∠AOB=30°,则△PMN周长的最小值为 E点是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,延长CE交AD.BA的延长线于F,G.求证:BCDF是等腰梯形.
E点是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,延长CE交AD.BA的延长线于F,G.求证:BCDF是等腰梯形.