题目内容
 如图,已知三角形木块ABC,∠A=30°,∠B=90°,AC=10cm,一只蚂蚁在AC、AB间往返爬行.当蚂蚁从木块AC边的中点O出发,爬行到AB边上任意一点P后,又爬回到AC边上的任意一点Q后,再爬行到点B,在这一过程中这只蚂蚁爬行的最短距离为
如图,已知三角形木块ABC,∠A=30°,∠B=90°,AC=10cm,一只蚂蚁在AC、AB间往返爬行.当蚂蚁从木块AC边的中点O出发,爬行到AB边上任意一点P后,又爬回到AC边上的任意一点Q后,再爬行到点B,在这一过程中这只蚂蚁爬行的最短距离为考点:轴对称-最短路线问题
专题:
分析:作O点关于AB的对称点M,作B点关于AC的对称点N,连接MN,交AB于P,交AC于Q,MN就是蚂蚁爬行的最短距离,根据轴对称的性质和SAS求得△OAK≌△BMK,得出BM=OA=5,∠A=∠KBM=30°,进而求得∠MBN=90°,根据30°的直角三角形的性质得出BM=BC,即可证得△ABC≌△NBM,从而得出MN的长.
解答: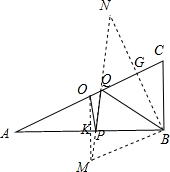 解:如图,作O点关于AB的对称点M,作B点关于AC的对称点N,连接MN,交AB于P,交AC于Q,MN就是蚂蚁爬行的最短距离,
解:如图,作O点关于AB的对称点M,作B点关于AC的对称点N,连接MN,交AB于P,交AC于Q,MN就是蚂蚁爬行的最短距离,
∴OP=MP,BQ=NQ,
∵AC=10,AO=CO,
∴OA=5,
∵OM⊥AB,∠B=90°,
∴OM∥BC,
∵AO=CO,
∴AK=BK,
在△OAK和△BMK中,
,
∴△OAK≌△BMK(SAS),
∴BM=OA=5,∠A=∠KBM=30°,
∵BN⊥AC,
∴∠ABG=60°,
∴∠MBN=90°,
∴AB=2BG=BN,
∵BC=
AC=5,
∴BM=BC,
在△ABC和△NBM中,
,
∴△ABC≌△NBM(SAS),
∴MN=AC=10cm.
故答案为10cm.
 解:如图,作O点关于AB的对称点M,作B点关于AC的对称点N,连接MN,交AB于P,交AC于Q,MN就是蚂蚁爬行的最短距离,
解:如图,作O点关于AB的对称点M,作B点关于AC的对称点N,连接MN,交AB于P,交AC于Q,MN就是蚂蚁爬行的最短距离,∴OP=MP,BQ=NQ,
∵AC=10,AO=CO,
∴OA=5,
∵OM⊥AB,∠B=90°,
∴OM∥BC,
∵AO=CO,
∴AK=BK,
在△OAK和△BMK中,
|
∴△OAK≌△BMK(SAS),
∴BM=OA=5,∠A=∠KBM=30°,
∵BN⊥AC,
∴∠ABG=60°,
∴∠MBN=90°,
∴AB=2BG=BN,
∵BC=
| 1 |
| 2 |
∴BM=BC,
在△ABC和△NBM中,
|
∴△ABC≌△NBM(SAS),
∴MN=AC=10cm.
故答案为10cm.
点评:本题考查的是轴对称-最短路线问题,熟知30°的直角三角形的性质三角形全等的判定和性质及两点直线线段最短是解答此题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
下列四个图形中,形成方法与另外三个不同的是( )
A、 |
B、 |
C、 |
D、 |
已知在△ABC中,∠C=90°,设sinA=m,当∠A是最小的内角时,m的取值范围是( )
A、0<m<
| ||||
B、0<m<
| ||||
C、0<m<
| ||||
D、0<m<
|
 E点是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,延长CE交AD.BA的延长线于F,G.求证:BCDF是等腰梯形.
E点是平行四边形ABCD内一点,已知DE⊥AD,∠CBE=∠CDE,∠BCE=45°,延长CE交AD.BA的延长线于F,G.求证:BCDF是等腰梯形.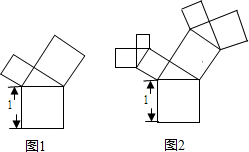 有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( )
有一个边长为1的正方形,经过一次“生长”后在它的上侧生长出两个小正方形(如图1),且三个正方形所围成的三角形是直角三角形;再经过一次“生长”后变成了图2,如此继续“生长”下去,则“生长”第k次后所有正方形的面积和为( ) 如图所示,两个天平都平衡,则与3个球体相等质量的正方体的个数为
如图所示,两个天平都平衡,则与3个球体相等质量的正方体的个数为