题目内容
如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
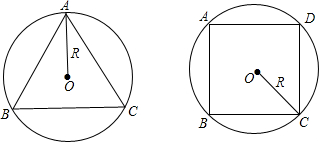

考点:正多边形和圆
专题:
分析:如图1,连接OB、OC,过O作OD⊥AB于D,求出中心角AOB,解直角三角形求出AD和OD,根据垂径定理求出AB,即可得出答案;连接OA、OB、OC,求出中心角COD,根据勾股定理求出CD,即可得出答案.
解答: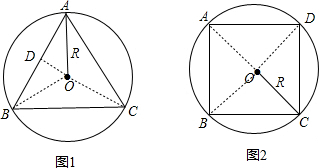 解:如图1,连接OB、OC,过O作OD⊥AB于D,
解:如图1,连接OB、OC,过O作OD⊥AB于D,
∵⊙O是正三角形ABC的外接圆,
∴∠AOB=
=120°,
∵OA=OB,
∴∠AOD=∠BOD=60°,
在Rt△ADO中,AO=R,AD=R×sin60°=
R,OD=Rcos60°=
R,
∵OD⊥AB,
∴AB=2AD=
R,
∴正△ABC的周长是3AB=3
R;面积是3×
AB×OD=3×
×
R×
R=
R2;
如图2,连接OA、OB、OD,
∵⊙O是正方形ABCD的外接圆,
∴∠COD=
=90°,
∵OD=OC=R,由勾股定理得;CD=
=
R,
∴正方形ABCD的周长为4×
R=4
R,面积为
R×
R=2R2.
 解:如图1,连接OB、OC,过O作OD⊥AB于D,
解:如图1,连接OB、OC,过O作OD⊥AB于D,∵⊙O是正三角形ABC的外接圆,
∴∠AOB=
| 360° |
| 3 |
∵OA=OB,
∴∠AOD=∠BOD=60°,
在Rt△ADO中,AO=R,AD=R×sin60°=
| ||
| 2 |
| 1 |
| 2 |
∵OD⊥AB,
∴AB=2AD=
| 3 |
∴正△ABC的周长是3AB=3
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 4 |
如图2,连接OA、OB、OD,
∵⊙O是正方形ABCD的外接圆,
∴∠COD=
| 360° |
| 4 |
∵OD=OC=R,由勾股定理得;CD=
| R2+R2 |
| 2 |
∴正方形ABCD的周长为4×
| 2 |
| 2 |
| 2 |
| 2 |
点评:本题考查了正多边形和圆,解直角三角形,正多边形的性质的应用,解此题的关键是求出正多边形的边长,主要考查学生的计算能力,难度适中.

练习册系列答案
相关题目
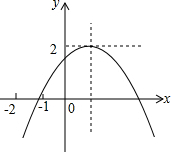 已知二次函数y=ax2+bx+c的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,以下结论:①b2-4ac>0,②abc<0,③m<2,④4a+c>2b中,正确的个数是( )
已知二次函数y=ax2+bx+c的图象如图所示,且关于x的一元二次方程ax2+bx+c-m=0没有实数根,以下结论:①b2-4ac>0,②abc<0,③m<2,④4a+c>2b中,正确的个数是( )| A、1 | B、2 | C、3 | D、4 |
下列代数式中符合书写要求的是( )
A、1
| ||
B、-
| ||
| C、a÷b | ||
| D、a2 |
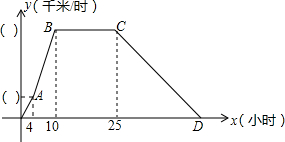 某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒地,风速变为平均每小时增加4千米/时,一段时间,风暴保持变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止.结合风速与时间的图象,回答下列问题:
某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒地,风速变为平均每小时增加4千米/时,一段时间,风暴保持变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止.结合风速与时间的图象,回答下列问题: