题目内容
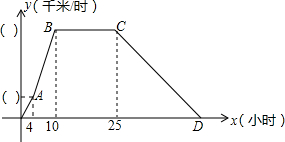 某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒地,风速变为平均每小时增加4千米/时,一段时间,风暴保持变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止.结合风速与时间的图象,回答下列问题:
某气象研究中心观测一场沙尘暴从发生到结束全过程,开始时风暴平均每小时增加2千米/时,4小时后,沙尘暴经过开阔荒地,风速变为平均每小时增加4千米/时,一段时间,风暴保持变,当沙尘暴遇到绿色植被区时,其风速平均每小时减小1千米/时,最终停止.结合风速与时间的图象,回答下列问题:(1)在y轴括号内填入相应的数值;
(2)沙尘暴从发生到结束,共经过多少小时?
(3)求出当x≥25时,风速y(千米/时)与时间x(小时)之间的函数关系式.
考点:一次函数的应用
专题:图表型
分析:(1)由速度=增加幅度×时间就可以求出结论;
(2)求出沙尘暴从开始减速到停止的时间+25小时;
(3)设线段CD的解析式为y=kx+b,由待定系数法求出其解即可.
(2)求出沙尘暴从开始减速到停止的时间+25小时;
(3)设线段CD的解析式为y=kx+b,由待定系数法求出其解即可.
解答:解:(1)由题意,得
2×4=8,
则8+4×(10-4)=32;
故答案为:8,32;
(2)由题意,得
32÷1+25=57小时;
答:沙尘暴从发生到结束,共经过57小时;
(3)设线段CD的解析式为y=kx+b,由题意,得
,
解得:
,
∴y=-x+57(25≤x≤57).
2×4=8,
则8+4×(10-4)=32;
故答案为:8,32;
(2)由题意,得
32÷1+25=57小时;
答:沙尘暴从发生到结束,共经过57小时;
(3)设线段CD的解析式为y=kx+b,由题意,得
|
解得:
|
∴y=-x+57(25≤x≤57).
点评:本题考查了匀加速运动的运用,待定系数法求一次函数的解析式的运用,解答时正确理解匀加速运动的含义,求函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是( )
二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是( )| A、ac>0 |
| B、b<0 |
| C、2a+b=0 |
| D、b2-4ac<0 |
 如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为akm和bkm,且张、李二村庄相距ckm.
如图,要在河边修建一个水泵站,分别向张村A和李庄B送水,已知张村A、李庄B到河边的距离分别为akm和bkm,且张、李二村庄相距ckm. 如图,用火柴棒搭正方形,搭x个正方形需要3001根火柴,写出含有x的方程.
如图,用火柴棒搭正方形,搭x个正方形需要3001根火柴,写出含有x的方程.