题目内容
11.计算:(1)5$\sqrt{12}$-9$\sqrt{\frac{1}{3}}$+$\frac{1}{2}$$\sqrt{48}$;
(2)(2$\sqrt{12}$-3$\sqrt{\frac{1}{3}}$)×$\sqrt{6}$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)先把各二次根式化为最简二次根式,然后把括号内合并后进行二次根式的乘法运算.
解答 解:(1)原式=10$\sqrt{3}$-3$\sqrt{3}$+2$\sqrt{3}$
=9$\sqrt{3}$;
(2)原式=(4$\sqrt{3}$-$\sqrt{3}$)×$\sqrt{6}$
=3$\sqrt{3}$×$\sqrt{6}$
=9$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
2.下列命题中,属于假命题的是( )
| A. | 两直线平行,同旁内角互补 | B. | 两直线平行,同位角相等 | ||
| C. | 等角的补角相等 | D. | 相等的角是对顶角 |
16.若分式$\frac{{x}^{2}-7x-8}{x+1}$的值为0,则x的值为( )
| A. | -1 | B. | 8 | C. | -1或8 | D. | -8 |
3.当x=$\frac{1}{3}$时,代数式$\frac{{x}^{2}-3x}{x-2}$÷($\frac{{x}^{2}}{x-2}$+$\frac{9}{2-x}$)的值是( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{10}$ | D. | $\frac{3}{10}$ |
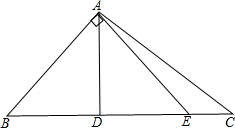 如图,在等腰直角△ABC中,AB=AC,∠BAC=90°,D、E是BC边上的点,且∠DAE=45°,试判断线段BD、DE和EC之间的数量关系,并证明你的结论.
如图,在等腰直角△ABC中,AB=AC,∠BAC=90°,D、E是BC边上的点,且∠DAE=45°,试判断线段BD、DE和EC之间的数量关系,并证明你的结论.