题目内容
15. 如图,圆O的半径为3,点A、B、C在圆O上,且∠ACB=45°,则弦AB的长是3$\sqrt{2}$.
如图,圆O的半径为3,点A、B、C在圆O上,且∠ACB=45°,则弦AB的长是3$\sqrt{2}$.
分析 首先连接OA,OB,由∠ACB=45°,易得△AOB是等腰直角三角形,继而求得弦AB的长.
解答  解:连接OA,OB,
解:连接OA,OB,
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB=3,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$.
点评 此题考查了圆周角定理以及等腰直角三角形性质.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
10.某班45名同学举行的“爱心涌动校园”募捐活动中捐款情况如下表所示
则该班捐款的平均数为24元.
| 捐款数(元) | 10 | 20 | 30 | 40 | 50 |
| 捐款人数(人) | 8 | 17 | 16 | 2 | 2 |
20. 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}-1$ |
4.下列命题中,是真命题的是( )
| A. | 长度相等的两条弧是等弧 | |
| B. | 顺次连结平行四边形四边中点所组成的图形是菱形 | |
| C. | 正八边形既是轴对称图形又是中心对称图形 | |
| D. | 三角形的内心到这个三角形三个顶点的距离相等 |
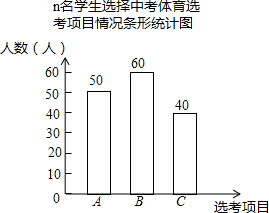 在学期初,某校体育组随机抽取了n名本校九年级学生,对这些学生选择中考体育选考项目进行问卷调查,问卷中的长春市中考体育选考项目包括:
在学期初,某校体育组随机抽取了n名本校九年级学生,对这些学生选择中考体育选考项目进行问卷调查,问卷中的长春市中考体育选考项目包括: