题目内容
李先生乘出租车去某公司办事，下车时，打出的电子收费单为“里程11千米，应收29.10元”．该城市的出租车收费标准按下表计算，请求出起步价N（N＜12）是（ ）
| 里程（公里） | 0＜x≤3 | 3＜x≤6 | x＞6 | ||||
| 价格（元） | N |
|
|
| A、9元 | B、8元 |
| C、10元 | D、11元 |
考点：一元二次方程的应用
专题：
分析：表格中的含义是：当行车里程不超过3公里时，价格是10元，当行车里程超过了3公里而不超过6公里时，除付10元外，超过的部分每公里再付
元；若行车里程超过6公里，除了需付以上两项费用外，超过6公里的部分，每公里再付
元．根据题意列出方程即可求解．
| 22 |
| N |
| 25 |
| N |
解答：解：依题意得N+（6-3）×
+（11-6）×
=29.10
整理得N2-29.1N+191=0
解得N1=19.1，N2=10
由于N＜12，所以N1=19.1舍去
则N=10
答：起步价是10元．
故选：C．
| 22 |
| N |
| 25 |
| N |
整理得N2-29.1N+191=0
解得N1=19.1，N2=10
由于N＜12，所以N1=19.1舍去
则N=10
答：起步价是10元．
故选：C．
点评：考查了一元二次方程的应用，读懂表格是正确列出方程的基础．找到关键描述语，找到等量关系准确的列出方程是解决问题的关键．
练习册系列答案
提分百分百检测卷系列答案
相关题目
均匀地向一个如图所示的容器中注水，最后把容器注满，在注水过程中水面高度h随时间变化的函数图象大致是（ ）
关于x的一元二次方程ax2+bx+c=0（a≠0），下列命题：
①若a、c异号，则方程 ax2+bx+c=0必有两个不相等的实数根；
②若4a-2b+c=0，则方ax2+bx+c=0有两个不等实根；
③若方程ax2+bx+c=0的两根互为相反数，则b=0；
④若b=a+c，则ax2+bx+c=0方程有两个不相等的实数根．
其中正确的为（ ）
①若a、c异号，则方程 ax2+bx+c=0必有两个不相等的实数根；
②若4a-2b+c=0，则方ax2+bx+c=0有两个不等实根；
③若方程ax2+bx+c=0的两根互为相反数，则b=0；
④若b=a+c，则ax2+bx+c=0方程有两个不相等的实数根．
其中正确的为（ ）
| A、①③ | B、①②③ |
| C、②③④ | D、①③④ |
下列运算正确的是（ ）
A、
| ||||||||||
B、
| ||||||||||
C、-4
| ||||||||||
D、
|
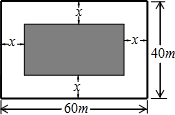如图，为了给小区居民增加锻炼场所，物业拟在一宽为40米、长为60米的矩形区域内的四周修建宽度相同的鹅卵石小路，阴影部分用作绿化．当阴影部分面积为800平方米时，小路宽x为多少米．