题目内容
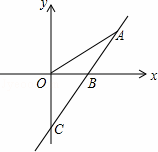
如图,直线y=kx﹣4与x轴,y轴分别交于B、C两点.且∠OBC=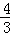 .
.
(1)求点B的坐标及k的值;
(2)若点A时第一象限内直线y=kx﹣4上一动点.则当△AOB的面积为6时,求点A的坐标;
(3)在(2)成立的条件下.在坐标轴上找一点P,使得∠APC=90°,直接写出P点坐标.
考点: 一次函数综合题.
分析: (1)由y=kx﹣4可知C(0,﹣4),即OC=4,根据tan∠OBC= ,得出OB=3,即可求得B的坐标为(3,0);
,得出OB=3,即可求得B的坐标为(3,0);
(2)根据题意可知直线为y= x﹣4,根据三角形的面积求得A的纵坐标,把A的纵坐标代入直线的解析式即可求得A的坐标;
x﹣4,根据三角形的面积求得A的纵坐标,把A的纵坐标代入直线的解析式即可求得A的坐标;
(3)分两种情况分别讨论即可求得.
解答: 解:(1)∵直线y=kx﹣4与x轴,y轴分别交于B、C两点,
∴OC=4,C(0,﹣4),
∵tan∠OBC= ,
,
∴OB=3,
∴B(3,0),
∴3k﹣4=0,
解得,k= ;
;
(2)如图2,

根据题意可知直线为y= x﹣4,
x﹣4,
∵S△AOB=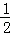 OB•yA,
OB•yA,
∴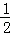 ×3×yA=6,解得yA═4,
×3×yA=6,解得yA═4,
∴把y=4代入y= x﹣4得,4=
x﹣4得,4= x﹣4,
x﹣4,
解得x=6,
∴A(6,4);
(3)如图2,作AD⊥x轴于D,
当P在y轴上时,∵∠APC=90°,
∴PA∥x轴,
∴OP=AD=4,
∴P(0,4),
当P在x轴上时,∵∠APC=90°,
∴∠APD+CPO=90°,
∴∠DAP=∠OPC,
∴△ADP∽△POC,
∴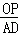 =
=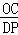 ,即
,即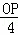 =
= ,
,
解得OP=﹣2或8,
∴P(﹣2,0)或(8,0),
综上,P的坐标为(0,4)或(﹣2,0)或(8,0).
点评: 本题是一次函数的综合题,考查了直角三角函数,三角形的面积,三角形相似的判定和性质,分类讨论思想的运用是解题的关键.

练习册系列答案
相关题目
 ,然后从-2、-1、0、1、2五个数中选取一个你喜欢的数作为
,然后从-2、-1、0、1、2五个数中选取一个你喜欢的数作为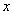 的值,求代数式的值.
的值,求代数式的值.


 B.
B.  C.
C.  D.
D. 
 =3 D. ﹣(﹣2)0=1
=3 D. ﹣(﹣2)0=1 =DC;
=DC;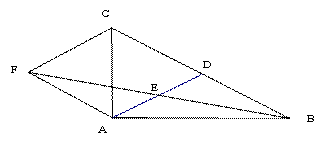 (2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.