题目内容
如图，正三角形ABC（图1）和正五边形DEFGH（图2）的边长相同．点O为△ABC的中心，用5个相同的△BOC拼入正五边形DEFGH中，得到图3，则图3中的五角星的五个锐角均为（ ）
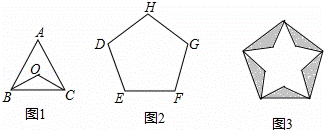
A． 36° B． 42° C． 45° D． 48°
D
考点： 多边形内角与外角；等边三角形的性质．
分析： 根据图1先求出正三角形ABC内大钝角的度数是120°，则两锐角的和等于60°，正五边形的内角和是540°，求出每一个内角的度数，然后解答即可．
解答： 解：如图，图1先求出正三角形ABC内大钝角的度数是180°﹣30°×2=120°，
180°﹣120°=60°，
60°÷2=30°，
正五边形的每一个内角=（5﹣2）•180°÷5=108°，
∴图3中的五角星的五个锐角均为：108°﹣60°=48°．
故选：D．
点评： 本题主要考查了多边形的内角与外角的性质，仔细观察图形是解题的关键，难度中等．
练习册系列答案
相关题目
形的共有（ ）
闲．宾馆需对游客居住的每个房间每天支出40元的各种费用．根据规定，要提高房价，但每个房间每天的房价不得高于280元．设每个房间的房价调整为每天x元（x为10的正
整数倍）．
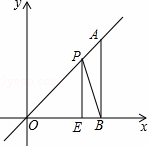
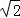B． 4+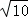
C． 6 D． 4
．
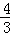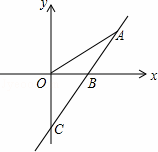
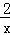（x＞0）的图象上有点A1，A2，A3，…，An﹣1，An，这些点的横坐标分别是1，2，3，…，n﹣1，n时，点A2的坐标是 ；过点A1作x轴的垂线，垂足为B1，再过点A2作A2P1⊥A1B1于点P1，以点P1、A1、A2为顶点的△P1A1A2的面积记为S1，按照以上方法继续作图，可以得到△P2A2A3，…，△Pn﹣1An﹣1An，其面积分别记为S2，…，Sn﹣1，则S1+S2+…+Sn= ．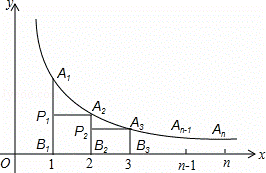
等于
B．
D．