题目内容
在Rt△ABC中,斜边AB=10,BC、AC是关于x的一元二次方程x2-2(m-1)+m(m-2)=0的两个根,求m的值.
考点:根与系数的关系,勾股定理
专题:
分析:由两根关系得BC+AC=2(m-1),BC•AC=m(m-2),由勾股定理得BC2+AC2=AB2,将等式变形,代入得出关于m的方程求解.
解答:解:根据题意得:BC+AC=2(m-1),BC•AC=m(m-2),
∵BC2+AC2=AB2,
即(BC+AC)2-2BC•AC=AB2,
∴(2m-2)2-2•m(m-2)=102,
解得m=-6或8,
∵BC+AC=2m-2>0,
∴m>1,
∴m=8.
∵BC2+AC2=AB2,
即(BC+AC)2-2BC•AC=AB2,
∴(2m-2)2-2•m(m-2)=102,
解得m=-6或8,
∵BC+AC=2m-2>0,
∴m>1,
∴m=8.
点评:本题考查了勾股定理及根与系数关系的综合运用.关键是由根与系数关系及勾股定理得出基本等式,再变形得出关于m的方程.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
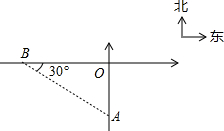 如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别?
如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别? 如图所示,已知△ABC中的∠ACB的外角平分线CD与∠ABC的平分线BD交于点D,过D作DE∥BC交AB于E,交AC于F,则有EF=BE-CF;试说明理由.
如图所示,已知△ABC中的∠ACB的外角平分线CD与∠ABC的平分线BD交于点D,过D作DE∥BC交AB于E,交AC于F,则有EF=BE-CF;试说明理由.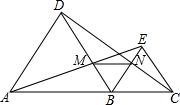 如图,A、B、C在同一直线上,且△ABD,△BCE都是等边三角形,AE交BD于点M,CD交BE于点N,求证:
如图,A、B、C在同一直线上,且△ABD,△BCE都是等边三角形,AE交BD于点M,CD交BE于点N,求证: