Question

1．如图，正方形ABCD的边长为4，E为BC上一点，BE=1，F为AB上一点，AF=2，P为AC上一点，则PF+PE的最小值为$\sqrt{17}$．

Answer 1

分析 作E关于直线AC的对称点E′，连接E′F，则E′F即为所求，过F作FG⊥CD于G，在Rt△E′FG中，利用勾股定理即可求出E′F的长．

解答 解：作E关于直线AC的对称点E′，连接E′F，则E′F即为所求，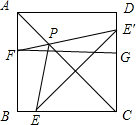

过F作FG⊥CD于G，
在Rt△E′FG中，
GE′=CD-BE-BF=4-1-2=1，GF=4，
所以E′F=$\sqrt{F{G}^{2}+E'{G}^{2}}=\sqrt{{1}^{2}+{4}^{2}}=\sqrt{17}$．
故答案为：$\sqrt{17}$．

点评 本题考查的是最短线路问题，熟知两点之间线段最短是解答此题的关键．