题目内容
3.已知$\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}3x+2y=m\\ nx-y=1\end{array}\right.$的解,则m+n的值是( )| A. | 1 | B. | 2 | C. | -2 | D. | 4 |
分析 把x与y的值代入方程组求出m与n的值,即可求出m+n的值.
解答 解:把$\left\{\begin{array}{l}x=-1\\ y=2\end{array}\right.$代入方程组得:$\left\{\begin{array}{l}3x+2y=m\\ nx-y=1\end{array}\right.$,
解得:m=1,n=-3,
则m+n=1-3=-2,
故选C.
点评 此题考查了二元一次方程组的解,方程组的解即为能使方程组中两方程成立的未知数的值.

练习册系列答案
相关题目
13.下列各组数中,能够组成直角三角形的是( )
| A. | 3,4,5 | B. | 4,5,6 | C. | 5,6,7 | D. | 6,7,8 |
14.若$\sqrt{x-1}$+(y+2)2=0,则(x+y)2017=( )
| A. | -1 | B. | 1 | C. | 32017 | D. | -32017 |
13.化简$\frac{x}{x-y}$$-\frac{y}{x+y}$的结果为( )
| A. | $\frac{2xy}{{x}^{2}-{y}^{2}}$ | B. | $-\frac{2xy}{{x}^{2}-{y}^{2}}$ | C. | $\frac{{x}^{2}+{y}^{2}}{{x}^{2}-{y}^{2}}$ | D. | 1 |
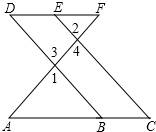 完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.
完成下面的证明.如图,E点位DF上的点,B为AC上的点,∠1=∠2,∠C=∠D,求证:DF∥AC.