题目内容
11.抛物线y=-2x2+3的图象上有两点A(x1,y1)、B(x2,y2),若0<x1<x2时,则y1、y2的大小是( )| A. | y1<y2 | B. | y1>y2 | C. | 0<y1<y2 | D. | 无法判断 |
分析 根据二次函数图象上点的坐标特征找出y1、y2的值,结合0<x1<x2,即可得知y1、y2的大小,此题得解.(借助于二次函数的性质找出其在x>0时的单调性亦可解决该问题)
解答 解:∵抛物线y=-2x2+3的图象上有两点A(x1,y1)、B(x2,y2),
∴y1=-2${{x}_{1}}^{2}$+3,y2=-2${{x}_{2}}^{2}$+3,
∵0<x1<x2,
∴${{x}_{1}}^{2}$<${{x}_{2}}^{2}$,
∴-2${{x}_{1}}^{2}$+3>-2${{x}_{2}}^{2}$+3,即y1>y2.
故选B.
点评 本题考查了二次函数图象上点的坐标特征,根据0<x1<x2找出y1、y2的大小是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.4的平方根是( )
| A. | ±2 | B. | -2 | C. | 2 | D. | $\sqrt{4}$ |
 如图,数轴上的有理数a,b,则|a+b|-|2a-c|=3a+b-c.
如图,数轴上的有理数a,b,则|a+b|-|2a-c|=3a+b-c.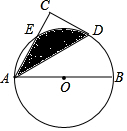 如图,AB为⊙O直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分面积是$\frac{2π}{3}$.
如图,AB为⊙O直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分面积是$\frac{2π}{3}$.