题目内容
1.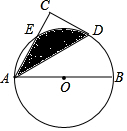 如图,AB为⊙O直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分面积是$\frac{2π}{3}$.
如图,AB为⊙O直径,CD切⊙O于点D,AC⊥CD交⊙O于点E,若∠BAC=60°,AB=4,则阴影部分面积是$\frac{2π}{3}$.
分析 如图,连接ED,OE,OD,由已知条件和切线的性质易证四边形AEDO是菱形,则△AEM≌△DMO,则图中阴影部分的面积=扇形EOD的面积.
解答 解:连接ED,OE,OD,设EO与AD交于点G,
∵⊙O切BC于D,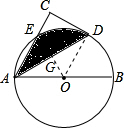
∴OD⊥BC,
∵AC⊥BC,
∴AC∥OD,
∵∠BAC=60°,OA=OE,
∴△AEO是等边三角形,
∴AE=OA,∠AOE=60°,
∴AE=AO=OD,
又∵AC∥OD即AE∥OD,
∴四边形AEDO是菱形,则△AEG≌△DGO,∠EOD=60°,
∴S△AEG=S△DGO,
∵AB=4,
∴AO=OD=2,
∴S阴影=S扇形EOD=$\frac{60π×4}{360}$=$\frac{2}{3}$π.
故答案为:$\frac{2}{3}$π.
点评 此题考查了切线的性质、菱形的判断和性质以及扇形面积公式的运用,此题难度适中,正确添加图形的助线是解题的关键.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.抛物线y=-2x2+3的图象上有两点A(x1,y1)、B(x2,y2),若0<x1<x2时,则y1、y2的大小是( )
| A. | y1<y2 | B. | y1>y2 | C. | 0<y1<y2 | D. | 无法判断 |
6.下列四个方程中,是一元一次方程的是( )
| A. | $\frac{1}{x}$=1 | B. | x+2=0 | C. | x2-1=1 | D. | x+y=6 |
10.某市今年新建绿化面积2743000m2,2743000用科学记数法表示为( )
| A. | 2.743×106 | B. | 27.43×105 | C. | 274.3×104 | D. | 2743×103 |
 如图,直线y=-$\frac{3}{4}$x+6与x轴交于C,与y轴交于A,过C、A分别作x轴,y轴的垂线交于点B,P是线段BC上的一个动点.
如图,直线y=-$\frac{3}{4}$x+6与x轴交于C,与y轴交于A,过C、A分别作x轴,y轴的垂线交于点B,P是线段BC上的一个动点. 如图,线段AB=22cm,C是AB上一点,且AC=14cm,O是AB的中点,线段OC=3cm.
如图,线段AB=22cm,C是AB上一点,且AC=14cm,O是AB的中点,线段OC=3cm.