题目内容
13.某日我舰艇停在港口A处准备进行搜救失联客机任务,突然收到消息有一股台风在其在正东方向200千米B处,正以$10\sqrt{5}$千米/时的速度向北偏西60°的方向移动,距台风中心150千米范围内是受台风影响区域(1)台风移动的过程中,我舰艇是否会受其影响?请写出结论并说明理由
(2)如果我舰艇受这次台风影响,那么受台风影响的时间有多长?
分析 (1)根据余角的定义,可得∠2的度数,根据直角三角形的性质,可得AC的长,根据有理数的大小比较,可得答案;
(2)根据勾股定理,可得CD的长,根据路程除以速度等于时间,可得答案.
解答 解:如图: ,
,
(1)台风移动的过程中,我舰艇会受其影响,理由如下:
∵∠1=60°,
∴∠2=30°.
∵∠ACB=90°,∠2=30°,AB=200千米,
∴AC=100千米<150千米,
∴台风移动的过程中,我舰艇会受其影响;
(2)在Rt△ACD中,由勾股定理,得
CD=$\sqrt{A{D}^{2}-A{C}^{2}}$=$\sqrt{15{0}^{2}-10{0}^{2}}$=50$\sqrt{5}$,
∵CE=CD=50$\sqrt{5}$千米,
∴DE=100$\sqrt{5}$千米,
100$\sqrt{5}$÷10$\sqrt{5}$=10(小时).
答:受台风影响的时间是10小时.
点评 本题考查了勾股定理的应用,利用了数形结合的思想,根据题意画出图形是解题关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
1.下列计算正确的是( )
| A. | 2a2+a2=3a4 | B. | a6•a2=a12 | C. | (-a6)2=a8 | D. | a6÷a2=a4 |
8. 如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
 如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )
如图,C、E和B、D、F分别在∠GAH的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF的度数为( )| A. | 75° | B. | 80° | C. | 85° | D. | 90° |
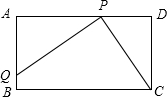 如图,在长方形ABCD中,AD=8,CD=4,P是AD上一点,且PA=PC.
如图,在长方形ABCD中,AD=8,CD=4,P是AD上一点,且PA=PC.