题目内容
20.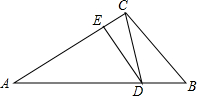 如图,△ABC中,AB=m,BC=n(m、n为常数,n<m).点D是AB上的一点,且∠DCB=∠A,过点D作DE∥BC于点E.
如图,△ABC中,AB=m,BC=n(m、n为常数,n<m).点D是AB上的一点,且∠DCB=∠A,过点D作DE∥BC于点E.(1)若m=8,n=4,试求BD;
(2)设△AED与△BCD的周长和为C,△ABC的周长为l.
探究:$\frac{C}{l}$的值是否存在最大或最小值?若存在,请求出这个值;若不存在,请说明理由.
分析 (1)证明△BCD∽△BAC,得出对应边成比例,即可求出BD的长;
(2)由平行线得出△ADE∽△ABC,由相似三角形的性质得出$\frac{{C}_{△ADE}}{{C}_{△ABC}}$=$\frac{BC}{AB}$,求出$\frac{C}{l}=\frac{{C}_{△ADE}+{C}_{△BCD}}{{C}_{△ABC}}$=$\frac{AD+BC}{AB}$,由(1)得:BD=$\frac{B{C}^{2}}{AB}$=$\frac{{n}^{2}}{m}$,得出$\frac{C}{l}$-($\frac{n}{m}$)2+$\frac{n}{m}$+1,由二次函数的最值即可得出当$\frac{n}{m}$=-$\frac{1}{-2}$=$\frac{1}{2}$时,即m=2n,$\frac{C}{l}$有最大值,求出最大值即可.
解答 解:(1)∵∠DCB=∠A,∠B=∠B,
∴△BCD∽△BAC,
∴$\frac{BD}{BC}=\frac{BC}{AB}$,即$\frac{BD}{4}=\frac{4}{8}$,
解得:BD=2;
(2)存在最大值;理由如下:
∵DE∥BC,
∴△ADE∽△ABC,
∴$\frac{{C}_{△ADE}}{{C}_{△ABC}}$=$\frac{BC}{AB}$,
∴$\frac{C}{l}=\frac{{C}_{△ADE}+{C}_{△BCD}}{{C}_{△ABC}}$=$\frac{AD+BC}{AB}$,
由(1)得:BD=$\frac{B{C}^{2}}{AB}$=$\frac{{n}^{2}}{m}$,
∴$\frac{C}{l}$=$\frac{m-\frac{{n}^{2}}{m}+n}{m}$=$\frac{{m}^{2}-{n}^{2}+mn}{{m}^{2}}$=1-($\frac{n}{m}$)2+$\frac{n}{m}$=-($\frac{n}{m}$)2+$\frac{n}{m}$+1,
当$\frac{n}{m}$=-$\frac{1}{-2}$=$\frac{1}{2}$时,即m=2n,$\frac{C}{l}$有最大值,最大值为$\frac{4×(-1)×1-{1}^{2}}{4×(-1)}$=$\frac{5}{4}$.
点评 本题是三角形综合题目,考查了相似三角形的判定与性质、二次函数的最值等知识;本题综合性强,有一定难度,证明三角形相似是解决问题的关键.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
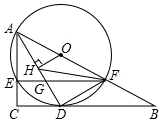 如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G.
如图,在Rt△ABC中,∠C=90°,点O在AB上,经过点A的⊙O与BC相切于点D,与AC,AB分别相交于点E,F,连接AD与EF相交于点G. 如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π).
如图,一扇形纸扇完全打开后,外侧两竹条AB和AC的夹角为120°,竹条AB的长为25cm,贴纸部分的宽BD为15cm,若纸扇两面贴纸,则一面贴纸的面积为175πcm2(结果保留π).