题目内容
10．某养鱼专业户准备挖一个面积为2000平方米的长方形鱼塘，设鱼塘的宽为x（米），长为y（米）．（1）写出y与x之间的函数关系式．
（2）当鱼塘的宽为20米时，求鱼塘的长．
分析 （1）直接利用矩形面积求法得出答案；
（2）利用（1）中所求，进而将x=20代入函数关系式得出答案．
解答 解：（1）由题意可得：xy=2000，
则y与x之间的函数关系式为：y=$\frac{2000}{x}$；
（2）当x=20时，y=$\frac{2000}{20}$=100，
当鱼塘的宽为20m时，鱼塘的长为100m．
点评 此题主要考查了反比例函数的应用，正确得出函数关系式是解题关键．
练习册系列答案
相关题目
17．
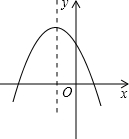已知二次函数y=ax2+bx+c的图象如图所示，那么下列结论：
①a＜0，②b＜0，③c＜0，
其中正确的判断是（ ）
已知二次函数y=ax2+bx+c的图象如图所示，那么下列结论：①a＜0，②b＜0，③c＜0，
其中正确的判断是（ ）
| A． | ①② | B． | ①③ | C． | ②③ | D． | ①②③ |
18．某学校初、高中六个年级共有3000名学生，为了解其视力情况，现采用抽样调查，各年级人数如下表所示：
（1）如果按10%的比例抽样，样本是什么？样本容量是多少？
（2）考虑到不同年级学生的视力差异，为了保证样本有较好的代表性，各年级分别应调查多少人？将结果填写在上面的表中；
（3）如果要从你所在的班50名学生中抽取5人进行调查，请设计一个抽样方案，保证每人有相同的机会被抽到．
| 年级 | 七年级 | 八年级 | 九年级 | 高一 | 高二 | 高三 | 合计 |
| 人数/名 | 560 | 520 | 500 | 500 | 480 | 440 | 3000 |
| 调查数/名 | 56 | 52 | 50 | 50 | 48 | 44 | 300 |
（2）考虑到不同年级学生的视力差异，为了保证样本有较好的代表性，各年级分别应调查多少人？将结果填写在上面的表中；
（3）如果要从你所在的班50名学生中抽取5人进行调查，请设计一个抽样方案，保证每人有相同的机会被抽到．
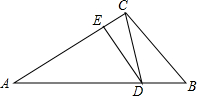如图，△ABC中，AB=m，BC=n（m、n为常数，n＜m）．点D是AB上的一点，且∠DCB=∠A，过点D作DE∥BC于点E．