题目内容
探究并证明以下问题:
(1)如图1,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点BO为线段上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP.
(2)如图2,在正方形ABCD中,点P为BC边上任意一点,以AP为边作正方形APMN,F为正方形APMN的中心,连结BF,直接写出BF与CP的数量关系 .
(3)如图3,在菱形ABCD中,AB:AC=m:n,点P为BC边上一点,以AP为对角线作菱形AFPM,满足∠ABC=∠AFP,连结BF,猜想BF与CP的数量关系,并证明你的结论.
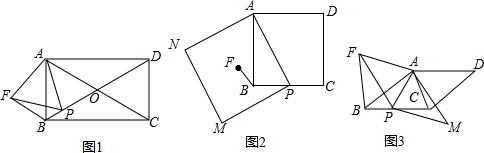
(1)如图1,矩形ABCD的对角线AC、BD交于点O,且∠AOB=60°,点BO为线段上任意一点,以AP为边作等边三角形APF.连结BF,求证:BF=OP.
(2)如图2,在正方形ABCD中,点P为BC边上任意一点,以AP为边作正方形APMN,F为正方形APMN的中心,连结BF,直接写出BF与CP的数量关系
(3)如图3,在菱形ABCD中,AB:AC=m:n,点P为BC边上一点,以AP为对角线作菱形AFPM,满足∠ABC=∠AFP,连结BF,猜想BF与CP的数量关系,并证明你的结论.

考点:四边形综合题
专题:
分析:(1)根据等边三角形的性质以及正方形的性质得出AB=AO,∠PAO=60°-∠BAP,进而证明△FAB≌△PAO即可得出答案;
(2)连接AC、AF、PF、BQ,过P作PQ⊥AC于Q,根据正方形的性质求出∠BFP=∠BQP,∠FBP=∠QPB,根据全等三角形的判定推出两三角形全等,根据全等三角形的性质求出BF=PQ,根据等腰直角三角形性质即可得出答案;
(3)首先利用菱形的性质得出,FA=FP,进而得出△FAP∽△BAC,以及△FAB∽△PAC,即可得出BF与CP的数量关系.
(2)连接AC、AF、PF、BQ,过P作PQ⊥AC于Q,根据正方形的性质求出∠BFP=∠BQP,∠FBP=∠QPB,根据全等三角形的判定推出两三角形全等,根据全等三角形的性质求出BF=PQ,根据等腰直角三角形性质即可得出答案;
(3)首先利用菱形的性质得出,FA=FP,进而得出△FAP∽△BAC,以及△FAB∽△PAC,即可得出BF与CP的数量关系.
解答: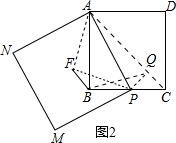 证明:(1)∵四边形ABCD为矩形,
证明:(1)∵四边形ABCD为矩形,
∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO,∠PAO=60°-∠BAP,
在△FAB和△PAO中,
,
∴△FAB≌△PAO(SAS),
∴BF=OP;
(2)连接AC、AF、PF、BQ,过P作PQ⊥AC于Q,
∵四边形ABCD是正方形,F为正方形APMN的中心,
∴∠ACB=∠APF=45°,∠AFP=∠ABC=90°,
∴A、F、B、P四点共圆,
∴∠ABF=∠ABF=45°,∠BFP=∠BAP,
同理∠ABP=∠AQP=90°,
∴∠ABP+∠AQP=180°,
∴∠BAP=∠BQP,
∴∠BFP=∠PQB,
∵PQ⊥AC,
∴∠QPC=∠ACB=45°,
∴∠FBP=∠QPB=90°+45°=135°,
在△FBP和△QPB中,
,
∴△FBP≌△QPB(AAS),
∴BF=PQ,
∵∠PQC=90°,∠ACB=∠QPC=45°,
∴PQ=
CP,
∴BF=
CP,
故答案为:BF=
CP.
(3)BF=
CP.
理由:∵四边形ABCD为菱形,
∴BA=BC,
∴∠BAC=
(180°-∠ABC),
∵四边形AFPM是菱形,
∴FA=FP,
∴∠FAP=
(180°-∠AFP),
∵∠ABC=∠AFP,
∴∠BAC=∠FAP,
∴△FAP∽△BAC,
∴
=
即
=
,
∵∠FAB=∠FAP-∠BAP,∠PAC=∠BAC-∠BAP,
∴∠FAB=∠PCA,
∴△FAB∽△PAC,
∴
=
=
,
即BF=
CP.
 证明:(1)∵四边形ABCD为矩形,
证明:(1)∵四边形ABCD为矩形,∴OA=OB,
∵∠AOB=60°,
∴△AOB是等边三角形,
∴AB=AO,∠PAO=60°-∠BAP,
在△FAB和△PAO中,
|
∴△FAB≌△PAO(SAS),
∴BF=OP;
(2)连接AC、AF、PF、BQ,过P作PQ⊥AC于Q,
∵四边形ABCD是正方形,F为正方形APMN的中心,
∴∠ACB=∠APF=45°,∠AFP=∠ABC=90°,
∴A、F、B、P四点共圆,
∴∠ABF=∠ABF=45°,∠BFP=∠BAP,
同理∠ABP=∠AQP=90°,
∴∠ABP+∠AQP=180°,
∴∠BAP=∠BQP,
∴∠BFP=∠PQB,
∵PQ⊥AC,
∴∠QPC=∠ACB=45°,
∴∠FBP=∠QPB=90°+45°=135°,
在△FBP和△QPB中,
|
∴△FBP≌△QPB(AAS),
∴BF=PQ,
∵∠PQC=90°,∠ACB=∠QPC=45°,
∴PQ=
| ||
| 2 |
∴BF=
| ||
| 2 |
故答案为:BF=
| ||
| 2 |
(3)BF=
| m |
| n |
理由:∵四边形ABCD为菱形,
∴BA=BC,
∴∠BAC=
| 1 |
| 2 |
∵四边形AFPM是菱形,
∴FA=FP,
∴∠FAP=
| 1 |
| 2 |
∵∠ABC=∠AFP,
∴∠BAC=∠FAP,
∴△FAP∽△BAC,
∴
| AF |
| AB |
| AP |
| AC |
| AF |
| AP |
| AB |
| AC |
∵∠FAB=∠FAP-∠BAP,∠PAC=∠BAC-∠BAP,
∴∠FAB=∠PCA,
∴△FAB∽△PAC,
∴
| BF |
| CP |
| AB |
| AC |
| m |
| n |
即BF=
| m |
| n |
点评:本题考查了正方形的性质,圆内接四边形的性质,全等三角形的性质和判定的应用,题目是一道综合性比较强的题目,有一定的难度.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是( )
| A、30cm2 |
| B、30πcm2 |
| C、15cm2 |
| D、15πcm2 |
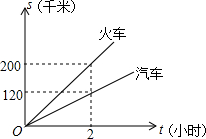 已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图.
已知A、B两地的路程为240千米,某经销商每天都要用汽车或火车将x吨保鲜品一次性由A地运往B地,受各种因素限制,下一周只能采用汽车和火车中的一种进行运输,且须提前预订,现有货运收费项目及收费标准表、行驶路程s(千米)与行驶时间t(时间)的函数图象,如图. 如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F.
如图,在△ABC中,AB=AC,BD=CD,DE⊥AB,DF⊥AC,垂足分别为点E、F. 在△ABC中,点E在AC上,且
在△ABC中,点E在AC上,且