题目内容
已知x+y=2,xy=2,求
x3y+x2y2+
xy3的值.
| 1 |
| 2 |
| 1 |
| 2 |
考点:提公因式法与公式法的综合运用
专题:
分析:先提取公因式-3,再对余下的多项式利用平方差公式继续分解.
解答:解:
x3y+x2y2+
xy3,
=
xy(x2+2xy+y2),
=
xy(x+y)2,
当x+y=2,xy=2时,原式=
×2×22=4.
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
当x+y=2,xy=2时,原式=
| 1 |
| 2 |
点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
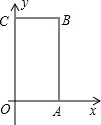 如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且
如图,矩形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(a,0)、(0,b),且 如图,EF交AD于O,AB交AD于A,CD交AD于D,∠1=∠2,∠3=∠4,试判AB和CD的位置关系,并说明为什么.
如图,EF交AD于O,AB交AD于A,CD交AD于D,∠1=∠2,∠3=∠4,试判AB和CD的位置关系,并说明为什么.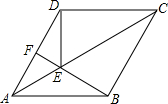 如图,点E是菱形ABCD对角线AC上的一点,连接BE,DE.
如图,点E是菱形ABCD对角线AC上的一点,连接BE,DE.