题目内容
19.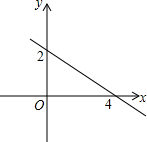 已知一次函数y=kx+b的图象如图所示,当x<1时,y的取值范围是( )
已知一次函数y=kx+b的图象如图所示,当x<1时,y的取值范围是( )| A. | 0<y<2 | B. | y<2 | C. | y>0 | D. | y>1.5 |
分析 运用待定系数法可求出一次函数的解析式,然后求出x=1所对应的y的值,再结合图象就可解决问题.
解答 解:把x=4,y=0;x=0,y=2代入y=kx+b得,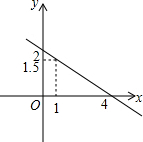
$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$,
∴y=-$\frac{1}{2}$x+2.
当x=1时,y=-$\frac{1}{2}$+2=1.5.
结合图象可得:
当x<1时,y的取值范围是y>1.5.
故选D.
点评 本题主要考查了运用待定系数法求一次函数的解析式、一次函数图象上点的坐标特征等知识,运用数形结合的思想是解决本题的关键.

练习册系列答案
相关题目
11.方程3x2+9=0的根是( )
| A. | x=-3 | B. | x=3 | C. | x=±3 | D. | 无实数根 |
 如图中共有2条直线,它们分别是直线AC,直线AB,图中以B端点的射线有3条,它们分别是射线BC,射线BD,射线BA.
如图中共有2条直线,它们分别是直线AC,直线AB,图中以B端点的射线有3条,它们分别是射线BC,射线BD,射线BA. 如图,一个圆锥的母线AB=2.5cm,底面半径OB=0.7cm,求它的高AO.
如图,一个圆锥的母线AB=2.5cm,底面半径OB=0.7cm,求它的高AO. 如图,直线AC,DE相交于点O,OE是∠AOB的平分线,∠COD=50°.试求∠AOB的度数.
如图,直线AC,DE相交于点O,OE是∠AOB的平分线,∠COD=50°.试求∠AOB的度数.