题目内容
 如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:其中正
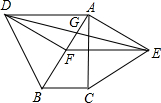
如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:其中正确结论的序号是
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④△DBF≌△EFA.
考点:全等三角形的判定与性质,等边三角形的性质,菱形的判定
专题:
分析:由等边三角形的性质及直角三角形的性质就可以得出△ADF≌△BAC,就可以求得四边形ADFE是平行四边形,由破晓四边形的性质而得出EF⊥AC,AD=4AG,就有△DBF≌△EFA.
解答:解:∵△ABD和△ACE都是等边三角形,
∴AD=BD=AB,AE=CE=AC,∠ADB=∠BAD=∠DBA=∠CAE=∠AEC=∠ACE=60°.
∵F是AB的中点,
∴∠BDF=∠ADF=30°,∠DFA=∠DFB=90°,BF=AF=
AB.
∵∠BAC=30°,∠ACB=90°,AD=2AF.
∴BC=
AB,∠ADF=∠BAC,
∴AF=BF=BC.
在Rt△ADF和Rt△BAC中
,
∴Rt△ADF≌Rt△BAC(HL),
∴DF=AC,
∴AE=AC.
∵∠BAC=30°,
∴∠BAC+∠CAE=∠BAE=90°,
∴∠DFA=∠EAB,
∴DF∥AE,
∴四边形ADFE是平行四边形,故②错误;
∴AD=EF,AD∥EF.
∴∠DAC=∠AHE.
∵∠DAC=∠DAB+∠BAC=90°,
∴∠AHE=90°,
∴EF⊥AC.①正确;
∵四边形ADFE是平行四边形,
∴2GF=2GA=AF.
∴AD=4AG.故③正确.
在Rt△DBF和Rt△EFA中
,
∴Rt△DBF≌Rt△EFA(HL).故④正确,
故答案为:①③④.
∴AD=BD=AB,AE=CE=AC,∠ADB=∠BAD=∠DBA=∠CAE=∠AEC=∠ACE=60°.
∵F是AB的中点,
∴∠BDF=∠ADF=30°,∠DFA=∠DFB=90°,BF=AF=
| 1 |
| 2 |
∵∠BAC=30°,∠ACB=90°,AD=2AF.
∴BC=
| 1 |
| 2 |
∴AF=BF=BC.
在Rt△ADF和Rt△BAC中
|
∴Rt△ADF≌Rt△BAC(HL),
∴DF=AC,
∴AE=AC.
∵∠BAC=30°,
∴∠BAC+∠CAE=∠BAE=90°,
∴∠DFA=∠EAB,
∴DF∥AE,

∴四边形ADFE是平行四边形,故②错误;
∴AD=EF,AD∥EF.
∴∠DAC=∠AHE.
∵∠DAC=∠DAB+∠BAC=90°,
∴∠AHE=90°,
∴EF⊥AC.①正确;
∵四边形ADFE是平行四边形,
∴2GF=2GA=AF.
∴AD=4AG.故③正确.
在Rt△DBF和Rt△EFA中
|
∴Rt△DBF≌Rt△EFA(HL).故④正确,
故答案为:①③④.
点评:本题考查了等边三角形的性质的运用,直角三角形的性质的运用,垂直的判定及性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,AB∥CD,设α=∠1+∠2+∠3,β=∠4+∠5,则α与β之间有怎样的数量关系?写出你的猜测和理由.
如图,AB∥CD,设α=∠1+∠2+∠3,β=∠4+∠5,则α与β之间有怎样的数量关系?写出你的猜测和理由.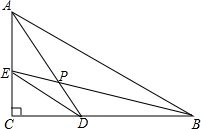 在△ABC中,∠C=90°,D、E分别是BC、CA上的点,且BD=AC,AE=CD,BE、AD相交于点P,则∠BPD=
在△ABC中,∠C=90°,D、E分别是BC、CA上的点,且BD=AC,AE=CD,BE、AD相交于点P,则∠BPD= 小明在拼图时,发现8个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,小红看见了,说:“我来试一试”.结果小红七拼八凑,拼成如图乙所示的正方形,怎么中间还留下一个洞,恰好是边长为2mm的小正方形!你能算出每个长方形的长和宽是多少吗?
小明在拼图时,发现8个一样大小的长方形恰好可以拼成一个大的长方形,如图甲所示,小红看见了,说:“我来试一试”.结果小红七拼八凑,拼成如图乙所示的正方形,怎么中间还留下一个洞,恰好是边长为2mm的小正方形!你能算出每个长方形的长和宽是多少吗?