题目内容
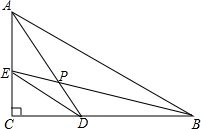 在△ABC中,∠C=90°,D、E分别是BC、CA上的点,且BD=AC,AE=CD,BE、AD相交于点P,则∠BPD=
在△ABC中,∠C=90°,D、E分别是BC、CA上的点,且BD=AC,AE=CD,BE、AD相交于点P,则∠BPD=考点:全等三角形的判定与性质
专题:
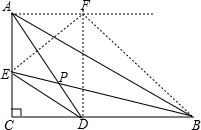
分析:作AF∥CD,DF∥AC,AF交DF于点F,连接EF,BF.就可以得出四边形ACDF是矩形,就可以得出AF=CD,DF=AC,就可以求出△AEF是等腰三角形和△BDF是等腰直角三角形,就可以得出△ADF∽△EBF就可以得出结论.
解答:解:作AF∥CD,DF∥AC,AF交DF于点F,
∴四边形ACDF是平行四边形.
∵∠C=90°
∴四边形ACDF是矩形,
∴CD=AF,AC=DF,∠EAF=∠FDB=∠AFD=90°.
∵BD=AC,AE=CD
∴△BDF和△AEF是等腰直角三角形,
∴∠AFE=∠DFB=45°,
∴∠DFE=45°,
∴∠EFB=90°.
∴∠EFB=∠AFD.
∴△BDF∽△AEF,
∴
=
 .
.
∵∠EFB=∠AFD,
∴△ADF∽△EBF
∴∠PAF=∠PEF
∴∠APE=∠AFE
∵∠AFE=45°
∴∠APE=45°
∴四边形ACDF是平行四边形.
∵∠C=90°
∴四边形ACDF是矩形,
∴CD=AF,AC=DF,∠EAF=∠FDB=∠AFD=90°.
∵BD=AC,AE=CD
∴△BDF和△AEF是等腰直角三角形,
∴∠AFE=∠DFB=45°,
∴∠DFE=45°,
∴∠EFB=90°.
∴∠EFB=∠AFD.
∴△BDF∽△AEF,
∴
| AF |
| DF |
| EF |
| BF |
 .
.∵∠EFB=∠AFD,
∴△ADF∽△EBF
∴∠PAF=∠PEF
∴∠APE=∠AFE
∵∠AFE=45°
∴∠APE=45°
点评:本题考查了矩形的性质的运用,等腰直角三角形的性质的运用,相似三角形的判定及性质的运用,解答时正确作出辅助线是关键.

练习册系列答案
相关题目
若-2x2-1与4x2-4x-5互为相反数,则( )
| A、x=-3或x=1 | ||||||||||||
B、x=1+
| ||||||||||||
| C、x=3或x=-1 | ||||||||||||
D、x=-1+
|
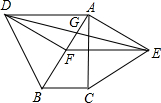 如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:其中正
如图,分别以Rt△ABC的斜边AB,直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB相交于点G,若∠BAC=30°,下列结论:其中正