题目内容
14. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | $\sqrt{6}$ |
分析 由于点B与D关于AC对称,所以BE与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,由正方形ABCD的面积为12,可求出AB的长,从而得出结果.
解答 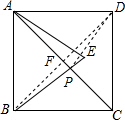 解:由题意,可得BE与AC交于点P.
解:由题意,可得BE与AC交于点P.
∵点B与D关于AC对称,
∴PD=PB,
∴PD+PE=PB+PE=BE最小.
∵正方形ABCD的面积为12,
∴AB=2$\sqrt{3}$.
又∵△ABE是等边三角形,
∴BE=AB=2$\sqrt{3}$.
故所求最小值为2$\sqrt{3}$.
故选B.
点评 此题考查了轴对称--最短路线问题,正方形的性质,等边三角形的性质,找到点P的位置是解决问题的关键.

练习册系列答案
相关题目
5.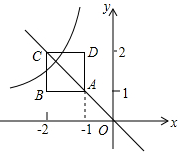 如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
 如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )
如图,正方形ABCD位于第二象限,AB=1,顶点A在直线y=-x 上,其中A点的横坐标为-1,且两条边AB、AD分别平行于x轴、y轴,若双曲线y=$\frac{k}{x}$(k≠0)与正方形ABCD有公共点.则k的取值范围是( )| A. | -4≤k≤-1 | B. | -4<k<-1 | C. | -4≤k<-1 | D. | 1≤k≤4 |
9. 将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
 将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )
将如图所示的几何图形,绕直线l旋转一周得到的立体图形( )| A. |  | B. |  | C. |  | D. |  |
3.为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
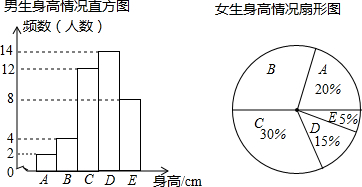
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在D组(填组别序号),女生身高在B组的人数有12人;
(2)在样本中,身高在150≤x<155之间的人数共有16人,身高人数最多的在C组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
| 组别 | 身高(cm) |
| A | x<150 |
| B | 150≤x<155 |
| C | 155≤x<160 |
| D | 160≤x<165 |
| E | x≥165 |

根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在D组(填组别序号),女生身高在B组的人数有12人;
(2)在样本中,身高在150≤x<155之间的人数共有16人,身高人数最多的在C组(填组别序号);
(3)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
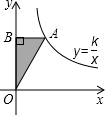 如图,已知A点是反比例函数y=$\frac{k}{x}$(k≠0)的图象上一点,AB⊥y轴于B,且△AOB的面积为2,则k的值为( )
如图,已知A点是反比例函数y=$\frac{k}{x}$(k≠0)的图象上一点,AB⊥y轴于B,且△AOB的面积为2,则k的值为( )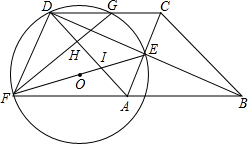 如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.
如图,四边形ABCD为菱形,对角线AC,BD相交于点E,F是边BA延长线上一点,连接EF,以EF为直径作⊙O,交DC于D,G两点,AD分别于EF,GF交于I,H两点.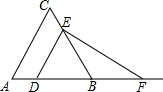 如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )