题目内容
6.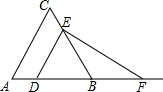 如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )
如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )| A. | 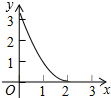 | B. |  | C. |  | D. |  |
分析 根据平行线的性质可得∠EDF=∠B=60°,根据三角形内角和定理即可求得∠F=30°,然后证得△EDB是等边三角形,从而求得ED=DB=2-x,再根据直角三角形的性质求得EF,最后根据三角形的面积公式求得y与x函数关系式,根据函数关系式即可判定.
解答 解:∵△ABC是等边三角形,
∴∠B=60°,
∵DE∥AC,
∴∠EDF=∠B=60°,
∵EF⊥DE,
∴∠DEF=90°,
∴∠F=90°-∠EDC=30°;
∵∠ACB=60°,∠EDC=60°,
∴△EDB是等边三角形.
∴ED=DB=2-x,
∵∠DEF=90°,∠F=30°,
∴EF=$\sqrt{3}$ED=$\sqrt{3}$(2-x).
∴y=$\frac{1}{2}$ED•EF=$\frac{1}{2}$(2-x)•$\sqrt{3}$(2-x),
即y=$\frac{\sqrt{3}}{2}$(x-2)2,(x<2),
故选A.
点评 本题考查了等边三角形的判定与性质,以及直角三角形的性质,特殊角的三角函数、三角形的面积等.

练习册系列答案
相关题目
16.-2015的绝对值是( )
| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
14. 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
 如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )
如图,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE最小,则这个最小值为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | $\sqrt{6}$ |
2.x与3的和的一半是正数,用不等式表示为( )
| A. | $\frac{1}{2}$x+3>0 | B. | $\frac{1}{2}$x+3<0 | C. | $\frac{1}{2}$(x+3)>0 | D. | $\frac{1}{2}$(x+3)<0 |
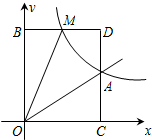 已知反比例函数$y=\frac{k}{x}$的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
已知反比例函数$y=\frac{k}{x}$的图象经过点A(2,1).点M(m,n)(0<m<2)是该函数图象上的一动点,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.
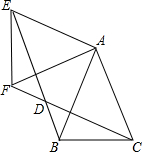 如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D.
如图,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D. 水平放置的容器内原有210毫米高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.
水平放置的容器内原有210毫米高的水,如图,将若干个球逐一放入该容器中,每放入一个大球水面就上升4毫米,每放入一个小球水面就上升3毫米,假定放入容器中的所有球完全浸没水中且水不溢出.设水面高为y毫米.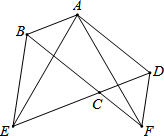 如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
如图,在?ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.