题目内容
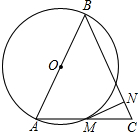 如图所示,在锐角△ABC中,AB=BC,点O是边AB的中点,以点O为圆心,OA为半径的圆交于点M,过点M作⊙O的切线MN交BC于点N.求证:CM2=CN•CB.
如图所示,在锐角△ABC中,AB=BC,点O是边AB的中点,以点O为圆心,OA为半径的圆交于点M,过点M作⊙O的切线MN交BC于点N.求证:CM2=CN•CB.考点:切线的性质,相似三角形的判定与性质
专题:
分析:连接BM、OM,根据等腰三角形的性质以及切线的性质证明∠MBC=∠CMN,证明△CMN∽△CBM,得到
=
,从而证得.
| CM |
| BC |
| CN |
| CM |
解答: 证明:连接BM、OM.
证明:连接BM、OM.
∵AB是直径,
∴∠AMB=90°,即BM⊥AC.
又∵AB=BC,
∴∠ABM=∠MBC,
∵MN是圆的切线,
∴OM⊥MN,即∠OMN=90°,
∴∠OMB=∠CMN,
∵OB=OC,
∴∠OMB=∠ABM,
∴∠MBC=∠CMN,
又∵∠C=∠C,
∴△CMN∽△CBM,
∴
=
,
∴CM2=CN•CB.
 证明:连接BM、OM.
证明:连接BM、OM.∵AB是直径,
∴∠AMB=90°,即BM⊥AC.
又∵AB=BC,
∴∠ABM=∠MBC,
∵MN是圆的切线,
∴OM⊥MN,即∠OMN=90°,
∴∠OMB=∠CMN,
∵OB=OC,
∴∠OMB=∠ABM,
∴∠MBC=∠CMN,
又∵∠C=∠C,
∴△CMN∽△CBM,
∴
| CM |
| BC |
| CN |
| CM |
∴CM2=CN•CB.
点评:本题考查了切线的性质定理以及等腰三角形的性质定理,和相似三角形的判定与性质,证明等积式成立,常用的方法是转化为证明比例式,然后转化为证明三角形相似.

练习册系列答案
相关题目
 根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )
根据生物学研究结果,青春期男女生身高增长速度呈现如图规律,由图可以判断,下列说法错误的是( )| A、男生在13岁时身高增长速度最快 |
| B、女生在10岁以后身高增长速度放慢 |
| C、11岁时男女生身高增长速度基本相同 |
| D、9-10岁时女生身高比男生身高要高 |
为了考察某校七年级800名学生的视力情况,从中抽取50名学生进行视力检查,这个问题中的样本是( )
| A、800名学生的视力 |
| B、抽取的50名学生 |
| C、抽取的50名学生的视力 |
| D、每个学生的视力 |
 一个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为
一个物体由多个完全相同的小正方体组成,它的三视图如图所示,那么组成这个物体的小正方体的个数为