题目内容
6. 如图,在平面直角坐标系中,等腰直角三角形ABC的腰长为2,直角顶点A在直线l:y=2x+2上移动,且斜边BC∥x轴,当△ABC在直线l上移动时,BC的中点D满足的函数关系式为( )
如图,在平面直角坐标系中,等腰直角三角形ABC的腰长为2,直角顶点A在直线l:y=2x+2上移动,且斜边BC∥x轴,当△ABC在直线l上移动时,BC的中点D满足的函数关系式为( )| A. | y=2x | B. | y=2x+1 | C. | y=2x+2-$\sqrt{2}$ | D. | y=2x-$\sqrt{2}$ |
分析 根据题意结合一次函数解析式得出ED的长,进而利用点D所在直线平行于y=2x+2所在直线,进而求出答案.
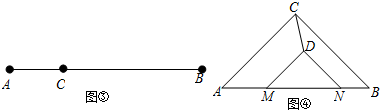
解答  解:如图所示:连接AD,BD交直线l:y=2x+2于点E,
解:如图所示:连接AD,BD交直线l:y=2x+2于点E,
∵AB=AC,D为BC的中点,
∴AD⊥BC,
∵BC∥x轴,
∴AD∥y轴,
∵y=2x+2当y=0,x=-1;当x=0,y=2,
∴$\frac{NO}{MO}$=$\frac{1}{2}$,
∴$\frac{ED}{AD}$=$\frac{1}{2}$,
∵AB=AC=2,
∴AD=$\sqrt{2}$,
∴ED=$\frac{\sqrt{2}}{2}$,
由题意可得点D所在直线平行于y=2x+2所在直线,
∴BC的中点D满足的函数关系式为:y=2(x-$\frac{\sqrt{2}}{2}$)+2=2x-$\sqrt{2}$+2.
故选:C.
点评 此题主要考查了一次函数图象上点的坐标性质以及一次函数的平移等知识,正确得出DE的长是解题关键.

练习册系列答案
相关题目
14.在平面直角坐标系中,点P(-2,3-π)所在象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.下列长度的各组线段中,能构成三角形的是( )
| A. | 3,4,5 | B. | 2,2,4 | C. | 1,2,3 | D. | 2,3,6 |
11.下列调查方式中,采用了“普查”方式的是( )
| A. | 调查某品牌手机的市场占有率 | |
| B. | 调查电视网(芈月传)在全国的收视率 | |
| C. | 调查我校初一(1)班的男女同学的比率 | |
| D. | 调查某型号节能灯泡的使用寿命 |
18.下列函数中(x是自变量)是二次函数的是( )
| A. | y=-$\frac{1}{2}+$x+$\frac{1}{x}$ | B. | y=1+x+5x2 | C. | y=22+2x | D. | y=$\frac{1}{2}{x}^{3}-{x}^{2}+25$ |