题目内容
18.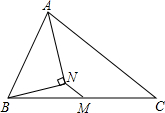 如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.
如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,求△ABC的周长.
分析 延长线段BN交AC于E,从而构造出全等三角形,(△ABN≌△AEN),进而证明MN是中位线,从而求出CE的长.
解答 解:延长线段BN交AC于E.
∵AN平分∠BAC,
在△ABN和△AEN中,
$\left\{\begin{array}{l}{∠BAN=∠EAN}\\{AN=AN}\\{∠ANB=∠ANE=90°}\end{array}\right.$
∴△ABN≌△AEN(ASA),
∴AE=AB=6,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×1.5=3,
∴△ABC的周长是AB+BC+AC=6+10+6+3=25.
点评 本题主要考查了中位线定理和全等三角形的判定.解决本题的关键是作出辅助线,利用全等三角形来得出线段相等,进而应用中位线定理解决问题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
9.下列命题中,真命题是( )
| A. | 相等的两个角是对顶角 | |
| B. | 内错角相等 | |
| C. | 垂线段最短 | |
| D. | 如果两条直线同时平行于第三条直线,那么这两条直线平行 |
6.下列二次根式中,与$\sqrt{2}$能合并的是( )
| A. | $\sqrt{24}$ | B. | $\sqrt{32}$ | C. | $\sqrt{96}$ | D. | $\sqrt{\frac{3}{4}}$ |
3. 某校在“爱护水资源”活动中组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布条形图.已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.那么在这次评比中,被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )
某校在“爱护水资源”活动中组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布条形图.已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.那么在这次评比中,被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )
 某校在“爱护水资源”活动中组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布条形图.已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.那么在这次评比中,被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )
某校在“爱护水资源”活动中组织学生进行社会调查,并对学生的调查报告进行了评比,如图是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频率分布条形图.已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.那么在这次评比中,被评为优秀的调查报告有(分数大于或等于80分为优秀,且分数为整数)( )| A. | 27篇 | B. | 25篇 | C. | 24篇 | D. | 18篇 |
10.某服装点用6000购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价),这两种服装的进价,标价如表所示.
(1)求这两种服装各购进的件数;
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
| 类型 价格 | A型 | B型 |
| 进价(元/件) | 60 | 100 |
| 标价(元/件) | 100 | 160 |
(2)如果A种服装按标价的8折出售,B种服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价出售少收入多少元?
 已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法:
已知,A市到B市的路程为260千米,甲车从A市前往B市运送物资,行驶2小时在M地汽车出现故障,立即通知技术人员乘乙车从A市赶来维修(通知时间忽略不计),乙车到达M地后又经过20分钟修好甲车后以原速原路返回A市,同时甲车以原来1.5倍的速度前往B市,如图是两车距A市的路程y(千米)与甲车所用时间x(小时)之间的函数图象,下列四种说法: