题目内容
如图，⊙M的圆心在x轴上，⊙M与坐标轴的交点A、B坐标分别是A（0，4），B（8，0），则点M坐标为考点：垂径定理,坐标与图形性质,勾股定理
专题：
分析：连接AM，设半径为r，构造直角三角形，利用勾股定理解答．
解答：
解：连接AM，设半径为r，
∵OM=8-r，AO=4，
∴在Rt△AOM中，（8-r）2+42=r2，
解得，r=5，
∴OM=8-5=3，
∴M（3，0）．
故答案为：（3，0）．
解：连接AM，设半径为r，∵OM=8-r，AO=4，
∴在Rt△AOM中，（8-r）2+42=r2，
解得，r=5，
∴OM=8-5=3，
∴M（3，0）．
故答案为：（3，0）．
点评：本题考查了垂径定理，构造直角三角形，利用勾股定理是解题关键．
练习册系列答案
相关题目
某商店第一次用600元购进某种铅笔若干支，第二次又用600元购进该种铅笔，但这次每支的进价比第一次贵1元，所以购进数量比第一次少了30支．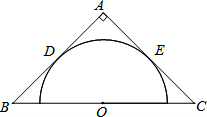
如图，在等腰直角三角形ABC中，AB=AC=8，O为BC的中点，以O为圆心作半圆，使它与AB，AC都相切，切点分别为D，E，则⊙O的半径为