题目内容
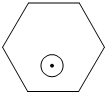 如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )| A、πr2 | ||||
B、
| ||||
C、2
| ||||
D、
|
考点:正多边形和圆,轨迹
专题:
分析:当⊙O运动到正六边形的角上时,圆与∠ABC两边的切点分别为E,F,连接OE,OF,OB,根据正六边形的性质可知∠ABC=120°,故∠OBF=60°,再由锐角三角函数的定义用r表示出BF的长,可知圆形纸片不能接触到的部分的面积=6×2S△BOF-S扇形EOF,由此可得出结论.
解答: 解:如图所示,连接OE,OF,OB,
解:如图所示,连接OE,OF,OB,
∵此多边形是正六边形,
∴∠ABC=120°,
∴∠OBF=60°.
∵∠OFB=90°,OF=r,
∴BF=
=
=
,
∴圆形纸片不能接触到的部分的面积
=6×2S△BOF-6S扇形EOF
=6×2×
×
r•r-6×
=2
r2-πr2.
故选C.
 解:如图所示,连接OE,OF,OB,
解:如图所示,连接OE,OF,OB,∵此多边形是正六边形,
∴∠ABC=120°,
∴∠OBF=60°.
∵∠OFB=90°,OF=r,
∴BF=
| OF |
| tan60° |
| r | ||
|
| ||
| 3 |
∴圆形纸片不能接触到的部分的面积
=6×2S△BOF-6S扇形EOF
=6×2×
| 1 |
| 2 |
| ||
| 3 |
| 60π×r2 |
| 360 |
=2
| 3 |
故选C.
点评:本题考查的是正多边形和圆,熟知正六边形的性质是解答此题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
 如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,若CD=8,AD=6,连接CC′,那么CC′的长是( )
如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,若CD=8,AD=6,连接CC′,那么CC′的长是( )| A、20 | ||
| B、100 | ||
C、10
| ||
D、10
|
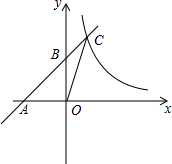 如图,直线y=
如图,直线y=
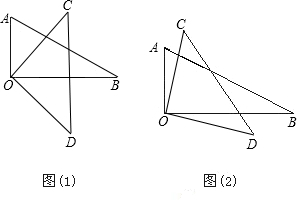 把一副三角板的直角顶点O重叠在一起.
把一副三角板的直角顶点O重叠在一起.