题目内容
 如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,若CD=8,AD=6,连接CC′,那么CC′的长是( )
如图,将矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,若CD=8,AD=6,连接CC′,那么CC′的长是( )| A、20 | ||
| B、100 | ||
C、10
| ||
D、10
|
考点:旋转的性质
专题:计算题
分析:先根据勾股定理计算出AC=10,再根据旋转的性质得AC=AC′,∠CAC′=90°,可判断△ACC′为等腰直角三角形,于是得到CC′=
AC=10
.
| 2 |
| 2 |
解答:解:∵四边形ABCD为矩形,
∴∠D=90°,
在Rt△ADC中,∵CD=8,AD=6,
∴AC=
=10,
∵矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,
∴AC=AC′,∠CAC′=90°,
∴△ACC′为等腰直角三角形,
∴CC′=
AC=10
.
故选D.
∴∠D=90°,
在Rt△ADC中,∵CD=8,AD=6,
∴AC=
| AD2+CD2 |
∵矩形ABCD绕点A顺时针旋转90°后,得到矩形AB′C′D′,
∴AC=AC′,∠CAC′=90°,
∴△ACC′为等腰直角三角形,
∴CC′=
| 2 |
| 2 |
故选D.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的性质.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
一个两位数的十位数字与个位数字之和是7,如果这两位数加上45,恰巧等于原数的个位数字与十位数字对调后所得的两位数,则原来的两位数为( )
| A、25 | B、16 | C、61 | D、34 |
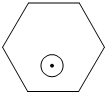 如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )| A、πr2 | ||||
B、
| ||||
C、2
| ||||
D、
|
 如图,在等边△ABC中,AD⊥BC,BE是中线,AD与BE交于点M.
如图,在等边△ABC中,AD⊥BC,BE是中线,AD与BE交于点M. 如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H.
如图,Rt△ABC的内切圆⊙O与AB、BC、CA分别相切于点D、E、F,且∠ACB=90°,AB=5,BC=3,点P是边AC上的一动点,PH⊥AB,垂足为H. 如图,在Rt△ABC中,∠ACB=90°,且点B的坐标为(-2,0).画出△ABC绕点O顺时针旋转90°后的△A1B1C1,并求点B旋转时所扫过的面积(结果保留π).
如图,在Rt△ABC中,∠ACB=90°,且点B的坐标为(-2,0).画出△ABC绕点O顺时针旋转90°后的△A1B1C1,并求点B旋转时所扫过的面积(结果保留π).