题目内容
将连续奇数1,3,5,7,9…排列成如图所示数表
(1)设中间的数为a,用式子表示十字框的五个数字之和.
(2)十字框中的五个数和能等于2015吗?若能,请写出这五个数;若不能,请说明理由.

(1)设中间的数为a,用式子表示十字框的五个数字之和.
(2)十字框中的五个数和能等于2015吗?若能,请写出这五个数;若不能,请说明理由.

考点:一元一次方程的应用
专题:
分析:(1)由图易知同一竖列相邻的两个数相隔16,横行相邻的两个数相隔2.用中间的数表示出其他四个数,然后相加即可;
(2)求出(1)中的代数式的和等于5a,可列方程求出中间的数,然后根据方程的解的情况就可以作出判断.
(2)求出(1)中的代数式的和等于5a,可列方程求出中间的数,然后根据方程的解的情况就可以作出判断.
解答:解:(1)设中间的数为a,则十字框的五个数字之和为:
a-16+a-2+a+a+2+a+16=5a.
故5个数字之和为5a;
(2)不能,
5a=2015,
解得a=403.
故十字框框住的5个数和能等于2015.
a-16+a-2+a+a+2+a+16=5a.
故5个数字之和为5a;
(2)不能,
5a=2015,
解得a=403.
故十字框框住的5个数和能等于2015.
点评:本题考查了一元一次方程的应用.此题注意结合数的排列规律发现左右和上下相邻两个数之间的大小关系,从而完成解答.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
若(3x+5)6=a6x6+a5x5+a4x4+a3x3+a2x2+a1x+a0,则-a6+a5-a4+a3-a2+a1-a0=( )
| A、1 | B、-1 | C、-64 | D、64 |
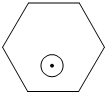 如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )| A、πr2 | ||||
B、
| ||||
C、2
| ||||
D、
|
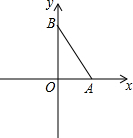 如图,点A、B分别在两条坐标轴上,且AB=2BO,在坐标轴上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )
如图,点A、B分别在两条坐标轴上,且AB=2BO,在坐标轴上取一点P,使得△PAB为等腰三角形,则符合条件的点P共有( )| A、5个 | B、6个 | C、7个 | D、8个 |
抛物线y=3x2-4x+1与x轴的交点的个数为( )
| A、0 | B、1 | C、2 | D、3 |
 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD=1,将△ACD沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则PB+PE的最小值是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD=1,将△ACD沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则PB+PE的最小值是 如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-2,-1),则点A坐标为
如图,平面直角坐标系中有一正方形OABC,点C的坐标为(-2,-1),则点A坐标为