题目内容
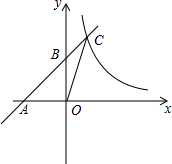 如图,直线y=
如图,直线y=| 1 |
| 2 |
| 4 |
| x |
考点:反比例函数与一次函数的交点问题
专题:证明题
分析:由直线解析式求得A、B的坐标,进而求得OA=2,OB=1,联立方程,解方程即可求得C的坐标,根据三角形的面积公式即可求得S△ABO=
OA•OB=
×2×1=1,S△BCO=
OB•|xC|=
×1×2=1,从而证得结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:由直线直线y=
x+1可知:A(-2,0),B(0,1),
∴OA=2,OB=1,
解
得
或
,
∴C(2,4),
∴S△ABO=
OA•OB=
×2×1=1,
S△BCO=
OB•|xC|=
×1×2=1,
∴S△ABO=S△BCO.
| 1 |
| 2 |
∴OA=2,OB=1,
解
|
|
|
∴C(2,4),
∴S△ABO=
| 1 |
| 2 |
| 1 |
| 2 |
S△BCO=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ABO=S△BCO.
点评:本题考查了反比例函数和一次函数的交点问题,求得交点坐标是本题的关键.

练习册系列答案
相关题目
(1)单项式
的系数是 ,次数是 ;
(2)2x3-y4-5x2y+4xy2最高次项系数是 ;
(3)设计一个二次三项式,使二次项系数为2,一次项系数为-2,常数项为
,这个二次三项式为 .
| -3a2b2 |
| 5 |
(2)2x3-y4-5x2y+4xy2最高次项系数是
(3)设计一个二次三项式,使二次项系数为2,一次项系数为-2,常数项为
| 1 |
| 2 |
下列计算正确的是( )
A、
| ||||||
B、3×
| ||||||
C、
| ||||||
D、
|
一个两位数的十位数字与个位数字之和是7,如果这两位数加上45,恰巧等于原数的个位数字与十位数字对调后所得的两位数,则原来的两位数为( )
| A、25 | B、16 | C、61 | D、34 |
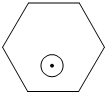 如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )
如图,一个半径为r(r<1)的圆形纸片在边长为10的正六边形内任意运动,则在该六边形内,这个圆形纸片不能接触到的部分的面积是( )| A、πr2 | ||||
B、
| ||||
C、2
| ||||
D、
|
 如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD=1,将△ACD沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则PB+PE的最小值是
如图,在Rt△ABC中,∠C=90°,∠ABC=30°,点D是BC边上的点,CD=1,将△ACD沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则PB+PE的最小值是 如图,在等边△ABC中,AD⊥BC,BE是中线,AD与BE交于点M.
如图,在等边△ABC中,AD⊥BC,BE是中线,AD与BE交于点M.