Question

7．在平面直角坐标系xOy中，一直线经过点A（-3，0），点B（0，$\sqrt{3}$），⊙P的圆心P的坐标为（1，0），与y轴相切于点O，若将⊙P沿x轴向左平移，平移后得到⊙P′，当⊙P′与直线相交时，横坐标为整数的点P′共有（　　）

• A． 1个
• B． 2个
• C． 3个
• D． 4个

Answer 1

分析 在解答本题时要先求出⊙P的半径，继而求得相切时P′点的坐标，根据A（-3，0），可以确定对应的横坐标为整数时对应的数值．

解答 解：如图所示，∵点P的坐标为（1，0），⊙P与y轴相切于点O，
∴⊙P的半径是1，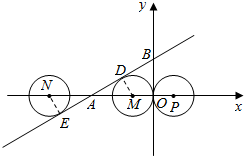
若⊙P与AB相切时，设切点为D，由点A（-3，0），点B（0，$\sqrt{3}$），
∴OA=3，OB=$\sqrt{3}$，由勾股定理得：AB=2$\sqrt{3}$，∠DAM=30°，
设平移后圆与直线AB第一次相切时圆心为M（即对应的P′），
∴MD⊥AB，MD=1，又因为∠DAM=30°，
∴AM=2，M点的坐标为（-1，0），即对应的P′点的坐标为（-1，0），
同理可得圆与直线第二次相切时圆心N的坐标为（-5，0），
所以当⊙P′与直线l相交时，横坐标为整数的点P′的横坐标可以是-2，-3，-4共三个．
故选：C．

点评 本题考查了圆的切线的性质的综合应用，解答本题的关键在于找到圆与直线相切时对应的圆心的坐标，然后结合A点的坐标求出对应的圆心的横坐标的整数解．