题目内容
已知实数a满足a2-3a+1=0,求下列各式的值:
(1)a+
的值;
(2)(a+
)2的值;
(3)a2+
的值;
(4)a4+
的值;
(5)(a-
)2的值;
(6)
的值;
(7)
的值;
(8)
的值.
(1)a+
| 1 |
| a |
(2)(a+
| 1 |
| a |
(3)a2+
| 1 |
| a2 |
(4)a4+
| 1 |
| a4 |
(5)(a-
| 1 |
| a |
(6)
| a2+5a+1 |
| a2-2a+1 |
(7)
| a2 |
| a4+1 |
(8)
| a2 |
| a4+a2+1 |
考点:分式的化简求值
专题:计算题
分析:(1)已知等式两边除以a变形求出a+
的值即可;
(2)把(1)结果两边平方即可;
(3)把(2)中结果利用完全平方公式变形即可;
(4)原式利用完全平方公式变形,把(3)中结果代入计算即可求出值;
(5)原式利用完全平方公式变形,把各自的值代入计算即可求出值;
(6)原式分子分母除以a变形,将a+
代入计算即可求出值;
(7)原式分子分母除以a2,把(3)中结果代入计算即可求出值;
(8)原式分子分母除以a2,把(3)中结果代入计算即可求出值.
| 1 |
| a |
(2)把(1)结果两边平方即可;
(3)把(2)中结果利用完全平方公式变形即可;
(4)原式利用完全平方公式变形,把(3)中结果代入计算即可求出值;
(5)原式利用完全平方公式变形,把各自的值代入计算即可求出值;
(6)原式分子分母除以a变形,将a+
| 1 |
| a |
(7)原式分子分母除以a2,把(3)中结果代入计算即可求出值;
(8)原式分子分母除以a2,把(3)中结果代入计算即可求出值.
解答:解:(1)a2-3a+1=0,变形得:a+
=3;
(2)∵a+
=3,
∴(a+
)2=9;
(3)a2+
=(a+
)2-2=9-2=7;
(4)a4+
=(a2+
)2-2=7-2=5;
(5)(a-
)2=a2+
-2=5-2=5;
(6)原式=
=
=8;
(7)原式=
=
;
(8)原式=
=
.
| 1 |
| a |
(2)∵a+
| 1 |
| a |
∴(a+
| 1 |
| a |
(3)a2+
| 1 |
| a2 |
| 1 |
| a |
(4)a4+
| 1 |
| a4 |
| 1 |
| a2 |
(5)(a-
| 1 |
| a |
| 1 |
| a2 |
(6)原式=
a+
| ||
a+
|
| 3+5 |
| 3-2 |
(7)原式=
| 1 | ||
a2+
|
| 1 |
| 7 |
(8)原式=
| 1 | ||
a2+
|
| 1 |
| 8 |
点评:此题考查了分式的化简求值,以及完全平方公式,熟练掌握完全平方公式是解本题的关键.

练习册系列答案
相关题目
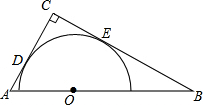 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则CD为
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则CD为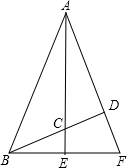 如图,在△ABC中,延长BC到D,延长AC到E,AD与BE相交于点F,∠ABC=45°,试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题,①AD⊥BD;②AE⊥BF;③AC=BF.
如图,在△ABC中,延长BC到D,延长AC到E,AD与BE相交于点F,∠ABC=45°,试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题,①AD⊥BD;②AE⊥BF;③AC=BF.