题目内容
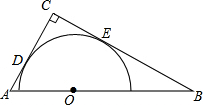如图，Rt△ABC中，∠ACB=90°，AC=4，BC=6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E，则CD为考点：切线的性质
专题：
分析：连接OD、OE，先设CD=x，再证明四边形ODCE是矩形，可得出OD=CE，OE=CD，从而得出OD=x，AD=4-x，可证明△AOD∽△ABC，再由比例式得出OD的长即可．
解答：
解：连接OD、OE，
设CD=x，
∵半圆分别与AC、BC相切，
∴∠CDO=∠CEO=90°，
∵∠C=90°，
∴四边形ODCE是矩形，
∴OD=CE，OE=CD，
又∵OD=OE，
∴AD=AC-CD=4-x，OD=x，
∵∠ADO=∠C=90°，∠DAO=∠CAB，
∴△AOD∽OABC，
∴
=
，
∴
=
，
解得x=2.4，
∴CD=2.4
故答案为2.4．
解：连接OD、OE，设CD=x，
∵半圆分别与AC、BC相切，
∴∠CDO=∠CEO=90°，
∵∠C=90°，
∴四边形ODCE是矩形，
∴OD=CE，OE=CD，
又∵OD=OE，
∴AD=AC-CD=4-x，OD=x，
∵∠ADO=∠C=90°，∠DAO=∠CAB，
∴△AOD∽OABC，
∴
| AD |
| AC |
| OD |
| BC |
∴
| 4-x |
| 4 |
| x |
| 6 |
解得x=2.4，
∴CD=2.4
故答案为2.4．
点评：本题考查了切线的性质．相似三角形的性质与判定，运用切线的性质来进行计算或论证，常通过作辅助线连接圆心和切点，利用垂直构造直角三角形，证明三角形相似解决有关问题．
练习册系列答案
习题精选系列答案
相关题目
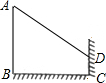一位同学想利用树影测量树高，他在某一时间测得长为1m的竹竿影长0.8m，但当他马上测量树影时，因树靠近一幢建筑物，影子不完全落在地面上，有一部分影子在墙上，如图所示，他先测得留在墙上的影高为1.2m，又测得地面部分的影长为5m，测算一下这棵树的高时多少？
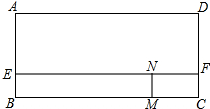如图，已知矩形ABCD，AB=6cm，BC=8cm，E、F分别是AB、CD上的点，且AE=DF=4cm，两动点M、N分别从C、F两点同时出发沿CB、FE均以2cm/s的速度向B、E两点运动，猜测当M、N运动多长时间，矩形CFNM与矩形AEFD相似？写出你的猜测过程，与同学交流．
如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，点P在边AB上，点Q在边BC上，且BQ=x，AP=2x（0＜x＜5），连接PQ．