题目内容
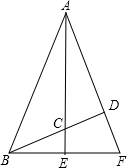 如图,在△ABC中,延长BC到D,延长AC到E,AD与BE相交于点F,∠ABC=45°,试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题,①AD⊥BD;②AE⊥BF;③AC=BF.
如图,在△ABC中,延长BC到D,延长AC到E,AD与BE相交于点F,∠ABC=45°,试选取下列条件中的两个作为题设,另一个作为结论组成一个正确命题,①AD⊥BD;②AE⊥BF;③AC=BF.(1)题设
(2)求证(1)中命题.
考点:全等三角形的判定与性质,命题与定理
专题:开放型
分析:(1)①②,③;
(1)易证AD=BD,∠DAC=∠EBC,即可证明△ACD≌△BFD,根据全等三角形对应边相等的性质即可解题.
(1)易证AD=BD,∠DAC=∠EBC,即可证明△ACD≌△BFD,根据全等三角形对应边相等的性质即可解题.
解答:解:(1)①②,③;
(2)证明:∵AD⊥BD,AE⊥BF,
∴∠ADC=∠BEC=∠BDF=90°,
又∵∠ABC=45°,
∴AD=BD,
∵∠DAC=180°-∠ADC-∠ACD,∠EBC=180°-∠BEC-∠BCE,∠BCE=∠ACD,
∴∠DAC=∠EBC,
∵在△ACD和△BFD中,
,
∴△ACD≌△BFD,(ASA)
∴AC=BF.
(2)证明:∵AD⊥BD,AE⊥BF,
∴∠ADC=∠BEC=∠BDF=90°,
又∵∠ABC=45°,
∴AD=BD,
∵∠DAC=180°-∠ADC-∠ACD,∠EBC=180°-∠BEC-∠BCE,∠BCE=∠ACD,
∴∠DAC=∠EBC,
∵在△ACD和△BFD中,
|
∴△ACD≌△BFD,(ASA)
∴AC=BF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△BFD是解题的关键.

练习册系列答案
相关题目
 某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示: 如图,∠1的两边分别为
如图,∠1的两边分别为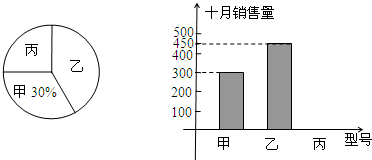
 如图,把一张长方形纸片沿AB折叠后,若∠1=50°,则∠2的度数为
如图,把一张长方形纸片沿AB折叠后,若∠1=50°,则∠2的度数为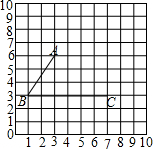 已知如图,请根据图形回答问题.
已知如图,请根据图形回答问题.