题目内容
5. 如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )
如图是一个正八边形,图中空白部分的面积等于20,则阴影部分的面积等于( )| A. | 20 | B. | $10\sqrt{2}$ | C. | 18 | D. | $20\sqrt{2}$ |
分析 设直角△AEF中,AE=x,则AF=x,EF=$\sqrt{2}$x,正八边形的边长是$\sqrt{2}$x.根据空白部分的面积是20即可列方程求得x的值,然后利用矩形和三角形的面积求解.
解答 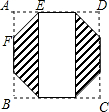 解:作出正方形ABCD.如图所示:
解:作出正方形ABCD.如图所示:
△AEF中,AE=x,则AF=x,EF=$\sqrt{2}$x,正八边形的边长是$\sqrt{2}$x.
则正方形的边长是(2+$\sqrt{2}$)x.
根据题意得:$\sqrt{2}$x(2+$\sqrt{2}$)x=20,
解得:x2=10($\sqrt{2}$-1).
则阴影部分的面积是:2[x(2+$\sqrt{2}$)x-2×$\frac{1}{2}$x2]=2($\sqrt{2}$+1)x2=2($\sqrt{2}$+1)×10($\sqrt{2}$-1)=20.
故选:A.
点评 本题考查了正多边形的计算,作出正方形,根据空白部分的面积,正确求得直角△AEF的直角边AE的长是关键.

练习册系列答案
相关题目
16. 某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
(说明:40---55分为不合格,55---70分为合格,70---85分为良好,85---100分为优秀)请根据以上信息,解答下列问题:
(1)表中的a=18,b=0.5;c=3;d=0.05
(2)请根据频数分布表,画出相应的频数分布直方图.
 某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表
某校为了更好的开展“学校特色体育教育”,从全校八年级各组随机抽取了60名学生,进行各项体育项目的测试,了解他们的身体素质情况.下表是整理样本数据,得到的关于每个个体的测试成绩的部分统计表、图:某校60名学生体育测试成绩频数分布表| 成绩 | 划记 | 频数 | 百分比 |
| 优秀 | 正正正 | a | 0.3 |
| 良好 | 正正正正正正 | 30 | b |
| 合格 | 正 | 9 | 0.15 |
| 不合格 | c | d | |
| 合计 |
(1)表中的a=18,b=0.5;c=3;d=0.05
(2)请根据频数分布表,画出相应的频数分布直方图.
13. 如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )
如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )
如图是一个正方体的表面展开图,则原正方体中与“创”字所在面相对的面的字是( )| A. | 城 | B. | 市 | C. | 卫 | D. | 生 |
17.若代数式x2-10x+k是一个完全平方式,则k=( )
| A. | 25 | B. | 25或-25 | C. | 10 | D. | 5或-5 |
14. 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
 如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )
如图,在△ABC中,AB=AC,∠A=40°,AB的垂直平分线MN交AC于D点,则∠DBC的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
15.下列方程中是一元一次方程的是( )
| A. | x-3=2x | B. | x2=1 | C. | 2x+y=1 | D. | $\frac{2}{x}$-1=0 |
 △ABC在直角坐标系中的位置如图所示,直线l经过点(1,0),并且与x轴垂直,△A1B1C1与△ABC关于线l对称.
△ABC在直角坐标系中的位置如图所示,直线l经过点(1,0),并且与x轴垂直,△A1B1C1与△ABC关于线l对称. 如图,点A、B的坐标分别为(0,3)、(4,6),点P为x轴上的一个动点,若点B关于直线AP的对称点B′恰好落在坐标轴上,则点B′的坐标为(-4,0)(0,-2)(0,8).
如图,点A、B的坐标分别为(0,3)、(4,6),点P为x轴上的一个动点,若点B关于直线AP的对称点B′恰好落在坐标轴上,则点B′的坐标为(-4,0)(0,-2)(0,8).