题目内容
8．用一些形状大小完全相同的：①等边三角形，②正方形，③正六边形，④正八边形．其中能镶嵌成平面图案的有（ ）| A． | 1种 | B． | 2种 | C． | 3种 | D． | 4种 |
分析 分别求出正三角形的每个内角是60°，正方形每个内角是90°，正六边形的每个内角是120°，正八边形的每个内角是135°，然后根据这些角的度数能否整除360度即可作出判断．
解答 解：①正三角形的每个内角是60°，能整除360°，能密铺；
②正方形每个内角是90°，能整除360°，能密铺；
③正六边形的每个内角是120°，能整除360°，能密铺；
④正八边形每个内角是180°-360°÷8=135°，不能整除360°，不能密铺．
故选C．
点评 本题考查平面镶嵌（密铺），知识点是：一种正多边形的镶嵌应符合一个内角度数能整除360°．
练习册系列答案
相关题目
18．
如图，将△ABC绕点C按顺时针方向旋转至△A′B′C′，使点A′落在BC的延长线上，已知∠A=30°，∠B=40°，则旋转角为（ ）
如图，将△ABC绕点C按顺时针方向旋转至△A′B′C′，使点A′落在BC的延长线上，已知∠A=30°，∠B=40°，则旋转角为（ ）| A． | 10° | B． | 35° | C． | 70° | D． | 110° |
19．下列命题正确的是（ ）
| A． | 对角线相等且互相平分的四边形是矩形 | |
| B． | 对角线互相垂直的四边形是菱形 | |
| C． | 菱形的面积等于对角线的积 | |
| D． | 平行四边形每条对角线平分一组对角 |
16．某学习小组10名学生参加数学竞赛，他们的得分情况如下表：
那么这10名学生所得分数的众数和中位数分别是（ ）
| 人数（人） | 2 | 3 | 4 | 1 |
| 分数（分） | 80 | 85 | 90 | 95 |
| A． | 90，90 | B． | 90，85 | C． | 90，87.5 | D． | 85，85 |
3．若（x+a）2=x2-10x+b，则a、b的值分别为（ ）
| A． | 2，4 | B． | 5，-25 | C． | -2，25 | D． | -5，25 |
13．
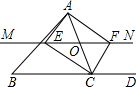如图，在△ABC中，O是AC上一动点，过点O作直线MN∥BC．设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，若点O运动到AC的中点，且∠ACB=（ ）时，则四边形AECF是正方形．
如图，在△ABC中，O是AC上一动点，过点O作直线MN∥BC．设MN交∠BCA的平分线于点E，交∠BCA的外角平分线于点F，若点O运动到AC的中点，且∠ACB=（ ）时，则四边形AECF是正方形．| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
20．关于?ABCD的叙述，正确的是（ ）
| A． | 若AB⊥BC，则?ABCD是菱形 | B． | 若AC⊥BD，则?ABCD是正方形 | ||
| C． | 若AC=BD，则?ABCD是矩形 | D． | 若AB=AD，则?ABCD是正方形 |
17．下列二次根式是最简二次根式的是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{10}$ | C． | $\sqrt{12}$ | D． | $\sqrt{18}$ |