题目内容
13.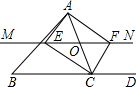 如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形.
如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC.设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F,若点O运动到AC的中点,且∠ACB=( )时,则四边形AECF是正方形.| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 由题意可得四边形AECF为一矩形,要使四边形AECF是正方形,只需添加一条件,使其邻边相等即可.
解答  解:过点E,F作EH⊥BD,FG⊥BD,
解:过点E,F作EH⊥BD,FG⊥BD,
∵CE,CF为∠ACB,∠ACD的角平分线,
∴∠ECF=90°.
∵MN∥BC,
∴∠FEC=∠ECH,
∵∠ECH=∠ECO,
∴∠FEC=∠ECO,
∴OE=OC.
同理OC=OF,
∴OE=OF,
∵点O运动到AC的中点,
∴OA=OC,
∴四边形AECF为一矩形,
若∠ACB=90°,则CE=CF,
∴四边形AECF为正方形.
故选:D.
点评 本题考查正方形的判定和性质、矩形的判定和性质、勾股定理等知识,熟练掌握这些知识是解决问题的关键,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3. 如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.
 如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.
如图,菱形ABCD的对角线AC,BD相交于点O,AC=8cm,BD=6cm,AC上一动点P从点C出发,沿CA方向以1cm/s的速度向A运动,设点P运动时间为ts.当t等于( )时,△PCD是直角三角形.| A. | $\frac{9}{4}$s | B. | 4s | C. | $\frac{9}{4}$s或$\frac{25}{4}$s | D. | 4s或$\frac{25}{4}$s |
4.若xm=16,xn=4,则x2m-3n的值为( )
| A. | 192 | B. | 8 | C. | -32 | D. | 4 |
1.实数-$\sqrt{2}$的倒数是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
8.用一些形状大小完全相同的:①等边三角形,②正方形,③正六边形,④正八边形.其中能镶嵌成平面图案的有( )
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
18.若$\sqrt{x+3}$有意义,则x能取的最小整数值是( )
| A. | 0 | B. | -2 | C. | -3 | D. | -4 |
2.不等式组1≤x<2的解集在数轴上可表示为( )
| A. |  | B. |  | C. |  | D. |  |
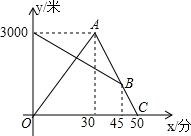 某天早晨,张强从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起按他返回时的速度回到家(张强和妈妈始终在同一条笔直的公路上).设两人离家的距离为y(米),张强出发的时间为x(分),y与x之间的函数图象如图所示.
某天早晨,张强从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,张强跑到体育场后发现要下雨,立即按原路返回,遇到妈妈后两人一起按他返回时的速度回到家(张强和妈妈始终在同一条笔直的公路上).设两人离家的距离为y(米),张强出发的时间为x(分),y与x之间的函数图象如图所示.