题目内容
（1+2+3+…+2013）（2+3+4+…+2012）-（1+2+3+…+2012）（2+3+4+…+2013）= ．
考点：有理数的混合运算
专题：
分析：设1+2+3+…+2012=a，则1+2+3+…+2013=a+2013，2+3+4+…+2012=a-1，2+3+4+…+2013=a+2012，由此简化计算即可．
解答：解：设1+2+3+…+2012=a，
原式=（a+2013）（a-1）-a（a+2012）
=a2+2012a-2013-a2-2012a
=-2013．
故答案为：-2013．
原式=（a+2013）（a-1）-a（a+2012）
=a2+2012a-2013-a2-2012a
=-2013．
故答案为：-2013．
点评：此题考查有理数的混合运算，掌握运算顺序，正确判定符号计算，注意整体思想的渗透．
练习册系列答案
相关题目
二次函数y=2x2-8x+1的对称轴与最小值是（ ）
| A、x=-2；-7 |
| B、x=2；-7 |
| C、x=2；9 |
| D、x=-2；-9 |
函数y=x，y=x2和y=
如图，在边长为xcm正方形纸片中剪去一个长为一辆汽车向南行驶5千米，再向南行驶-5千米，结果是（ ）
| A、向南行驶10千米 |
| B、向北行驶5千米 |
| C、回到原地 |
| D、向北行驶10千米 |
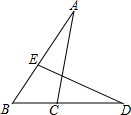如图，△ABC≌△DBE，AB与DB，AC与DE是对应边，已知：∠B=43°，∠A=30°，求∠BED的度数．请你完善下面的推理步骤：解：∵∠A+∠B+∠BCA=180°（