题目内容
9.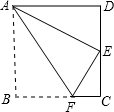 如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm,DE:EC=3:2,则FC的长度为3cm.
如图,一张矩形纸片ABCD,沿AF折叠,点B恰好落在CD边上的点E处,已知CD为10cm,DE:EC=3:2,则FC的长度为3cm.
分析 由矩形的性质和折叠的性质得出∠C=∠D=90°AE=AB=10cm,EF=BF,由勾股定理求出AD,得出BC,设FC=xcm,则EF=BF=(8-x)cm,根据勾股定理得出方程,解方程即可.
解答 解:,∵四边形ABCD是矩形,
∴∠C=∠D=90°,AB=CD=10cm,BC=AD,
根据折叠的性质得:AE=AB=10cm,EF=BF,
∵DE:EC=3:2,
∴DE=6cm,EC=4cm,
∴AD=$\sqrt{A{E}^{2}-D{E}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8(cm),
∴BC=8cm,
设FC=xcm,则EF=BF=(8-x)cm,
根据勾股定理得:FC2+EC2=EF2,
即x2+42=(8-x)2,
解得:x=3,
∴FC=3cm.
故答案为:3.
点评 本题考查了矩形的性质、翻折变换的性质、勾股定理;熟练掌握矩形的性质和翻折变换的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
17.下列四个关系式:(1)y=x;(2)y=x2;(3)y=x3;(4)|y|=x,其中y不是x的函数的是( )
| A. | (1) | B. | (2) | C. | (3) | D. | (4) |
4.下列说法正确的是( )
| A. | 平移不改变图形的形状和大小,而旋转则改变图形的形状和大小 | |
| B. | 平移和旋转的共同点是改变了图形的位置,而图形的形状大小没有变化 | |
| C. | 图形可以向某方向平移一定距离,也可以向某方向旋转一定距离 | |
| D. | 在平移和旋转图形中,对应角相等,对应线段相等且平行 |
14.已知y是关于x的反比例函数,点P(x1,y1),Q(x2,y2)是反比例函数图象上的点,则下列结论正确的是( )
| A. | x1+y1=x2+y2 | B. | x1y2=x2y1 | C. | $\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$ | D. | $\frac{{x}_{2}}{{x}_{1}}$=$\frac{{y}_{1}}{{y}_{2}}$ |
18.下列说法中,错误的是( )
| A. | (-4)2的平方根是-4 | B. | 5是25的算术平方根 | ||
| C. | -$\frac{1}{3}$是-$\frac{1}{27}$的立方根 | D. | -$\frac{5}{6}$是$\frac{25}{36}$的一个平方根 |
19.如图是小李书桌上放的一本书,则这本书的俯视图是( )


| A. |  | B. |  | C. |  | D. |  |