题目内容
4．与2和为0的数是（ ）| A． | -2 | B． | 2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
分析 根据相反数的意义即可得出答案．
解答 解∵-2+2=0，
∴与2的和为0的数是-2；
故选A．
点评 本题主要考查了相反数，掌握相反数的意义是本题的关键，只有符号不同的两个数互为相反数，a的相反数是-a．
练习册系列答案
相关题目
；
；
；
，
17．把分式$\frac{{2xy+3{y^2}}}{y^2}$中的x，y同时扩大2倍，则分式的值（ ）
| A． | 扩大2倍 | B． | 改变 | C． | 缩小2倍 | D． | 不改变 |
14．
如图，直线AB、CD、EF相交于一点，∠1=50°，∠2=64°，则∠COF=（ ）度．
如图，直线AB、CD、EF相交于一点，∠1=50°，∠2=64°，则∠COF=（ ）度．| A． | 66 | B． | 50 | C． | 64 | D． | 76 |
19．下面图形中，是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
9．
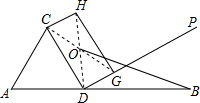如图，线段AB的长为20，点D在AB上，△ACD是边长为8的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值为（ ）
如图，线段AB的长为20，点D在AB上，△ACD是边长为8的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH的对角线交点为O，连接OB，则线段BO的最小值为（ ）| A． | 10 | B． | 6 | C． | 8$\sqrt{3}$ | D． | 6$\sqrt{3}$ |
如图，在△ABC中，点E、D、F分别在边AB、BC、CA上，且DE∥CA，DF∥BA，下列四个判断中，正确的个数有 （ ）
13．已知关于x的一元二次方程x2+ax+b=0有一个非零根b，则a+b的值为（ ）
| A． | 1 | B． | -1 | C． | 0 | D． | 一2 |
13．已知a，b，c分别是△ABC的三边长，且满足2a4+2b4+c4-2a2c2-2b2c2=0，则△ABC是（ ）
| A． | 等腰三角形 | B． | 等腰直角三角形 | ||
| C． | 直角三角形 | D． | 等腰三角形或直角三角形 |