题目内容
甲、乙两人玩猜数字游戏，游戏规则如下：有三个数字0、1、3，先由甲在心中任选一个数字，记为m，再由乙猜甲刚才所选的数字，记为n．若m、n满足|m-n|≤1，则称甲、乙两人“心有灵犀”，求甲、乙两人“心有灵犀”的概率．（用树状图或列表法求解）
考点：列表法与树状图法
专题：
分析：首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲、乙两人“心有灵犀”的情况，再利用概率公式即可求得答案．
解答：解：画树状图得：
∵共有9种等可能的结果，甲、乙两人“心有灵犀”的有5种情况，
∴甲、乙两人“心有灵犀”的概率为：
．
∵共有9种等可能的结果，甲、乙两人“心有灵犀”的有5种情况，
∴甲、乙两人“心有灵犀”的概率为：
| 5 |
| 9 |
点评：本题考查的是用列表法或画树状图法求概率．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
如图，Rt△ADB中，∠D=90°，∠A=32°，C为边AD上一点，C与点A、D不重合，设∠ACB的度数为x，则x的取值范围是已知实数x、y满足2
+3（y+1）2=0，则x-y=（ ）
| x-2 |
| A、3 | B、-3 | C、1 | D、-1 |
如图，在正方形ABCD中，点E、F分别在边AB、BC上，∠ADE=∠CDF．
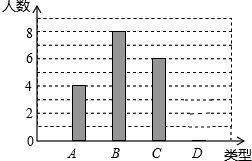某校240名学生参加植树活动，要求每人植树4～7棵，活动结束后抽查了20名学生每人的植树量，并分为四类：A类4棵、B类5棵、C类6棵、D类7棵，将各类的人数绘制成如图所示不完整的条形统计图，回答下列问题：