题目内容
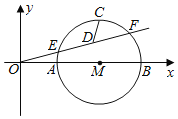
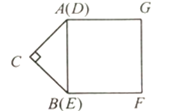
【题目】如图,等腰![]() 的
的![]() 边与正方形
边与正方形![]() 的
的![]() 边重合,
边重合,![]() .
.![]() 从如图所示位置水平向右匀速运动,直到点
从如图所示位置水平向右匀速运动,直到点![]() 落在边
落在边![]() 上.设
上.设![]() ,运动过程中
,运动过程中![]() 与正方形
与正方形![]() 的重合部分面积为
的重合部分面积为![]() ,则能反映
,则能反映![]() 与
与![]() 的函数关系的图象是( )
的函数关系的图象是( )
A. B.
B.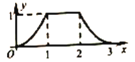
C.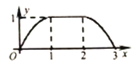 D.
D.
【答案】D
【解析】
由于△ABC是等腰直角三角形,依题意知道在开始移动时△ABC与正方形DEFG重叠部分的面积逐渐增加,当点![]() 落在边DE边上,直到AB与GF重合,面积保持不变,之后面积开始逐渐减小,△ABC与正方形DEFG重叠部分的面积y与x函数的关系式函数二次函数,利用这些结论即可求解
落在边DE边上,直到AB与GF重合,面积保持不变,之后面积开始逐渐减小,△ABC与正方形DEFG重叠部分的面积y与x函数的关系式函数二次函数,利用这些结论即可求解
∵△ABC是等腰直角三角形,
依题意知在开始移动时△ABC与正方形DEFG重叠部分的面积逐渐增加,
∴![]()
当点![]() 落在边DE边上,直到AB与GF重合,面积保持不变,
落在边DE边上,直到AB与GF重合,面积保持不变,
![]()
之后面积开始逐渐减小,
![]()
D选项符合题意,
故选:D.

练习册系列答案
相关题目
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?