Question

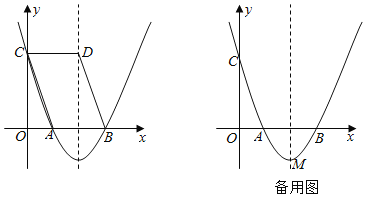
【题目】在平面直角坐标系中，抛物线与轴交于点．

（1）求点的坐标（用含的式子表示）；

（2）求抛物线与轴的交点坐标；

（3）已知点，，如果抛物线与线段恰有一个公共点，结合函数图象，求的取值范围．

Answer 1

【答案】（1）的坐标为．（2），．（3）或．

【解析】

（1）令，即可求出A点的纵坐标，从而得到答案；

（2）令，即可求抛物线与轴的交点的纵坐标，从而得到答案；

（3）分和两种情况讨论，时，；时，由①知时，点始终在点的下方，所以抛物线与线段恰有一个公共点时，只要即可．

（1）令，则．

∴点的坐标为．

（2）令，则．

∵，∴解得，．

∴抛物线与轴的交点坐标分别为，．

（3）①当时，

可知，

解得．

∴的取值范围是．

②当时，由①知时，点始终在点的下方，所以抛物线与线段恰有一个公共点时，只要即可．

综上所述，的取值范围是或．