题目内容
【题目】“互联网+”时代,网上购物备受消费者青睐.某网店专售一种商品,其成本为每件![]() 元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
元,已知销售过程中,销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]() .据市场调查发现,月销售量
.据市场调查发现,月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如表:
(元)之间的函数关系如表:
销售单价 | 65 | 70 | 75 | 80 | ··· |
月销售量 | 475 | 450 | 425 | 400 | ··· |
![]() 请根据表格中所给数据,求出
请根据表格中所给数据,求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
![]() 设该网店每月获得的利润为
设该网店每月获得的利润为![]() 元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
元,当销售单价为多少元时,每月获得的利润最大,最大利润是多少?
![]() 该网店店主热心公益事业,决定每月从利润中捐出
该网店店主热心公益事业,决定每月从利润中捐出![]() 元资助贫困学生.为了保证捐款后每月利润不低于
元资助贫困学生.为了保证捐款后每月利润不低于![]() 元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
元,且让消费者得到最大的实惠,该如何确定该商品的销售单价?
【答案】(1)![]() ;(2)当销售单价
;(2)当销售单价![]() 为
为![]() 元时,每月获得的利润最大,最大利润是
元时,每月获得的利润最大,最大利润是![]() 元;(3)
元;(3)![]() 元
元
【解析】
(1)先根据表格猜测![]() 与
与![]() 的函数关系是一次函数,再运用待定系数法求解即可;
的函数关系是一次函数,再运用待定系数法求解即可;
(2)根据销售问题公式:销售利润=单件利润×销售量即可列出二次函数解析式,再根据二次函数的顶点式即可求解;
(3)根据(2)所列函数解析式,把w=7700+300代入即可求解.
解:![]() 根据表格中的数据猜想
根据表格中的数据猜想![]() 与
与![]() 的函数关系是一次函数
的函数关系是一次函数
![]() 设
设![]() ,将
,将![]() 代入
代入![]() ,得
,得
![]()
解得![]()
![]()
经验证,![]() 都满足上述函数关系式
都满足上述函数关系式
答:![]() 与
与![]() 的函数关系式为
的函数关系式为![]()
![]() 由题意,得
由题意,得![]()
![]()
![]()
![]()
![]() 销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于
销售单价不低于成本单价,且物价部门规定这种商品的获利不得高于![]()
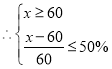
![]()
![]()
∴抛物线开口向下,对称轴为直线![]()
![]()
![]() 此时函数图象在对称轴的左侧,
此时函数图象在对称轴的左侧,
![]() 随
随 ![]() 的增大而增大
的增大而增大
![]() 时,
时,
![]() 取得最大值,
取得最大值,![]()
答:当销售单价![]() 为
为![]() 元时,每月获得的利润最大,最大利润是
元时,每月获得的利润最大,最大利润是![]() 元
元
![]() 根据题意得
根据题意得![]()
解得:![]()
![]() 抛物线开口向下
抛物线开口向下
∴当![]() 时,
时,
每月利润不低于![]() 元
元
又![]()
![]() 当
当![]() 时,
时,
每月利润不低于![]() 元
元
![]() 要让消费者得到最大的实惠
要让消费者得到最大的实惠
![]()
答:该商品的销售单价定为![]() 元时,符合该网店要求且让消费者得到最大的实惠
元时,符合该网店要求且让消费者得到最大的实惠

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】疫情无情人有情,爱心捐款传真情.新冠肺炎疫情发生后,某班学生积极参加献爱心活动,该班![]() 名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
名学生的捐款统计情况如下表,关于捐款金额,下列说法错误的是( )
金额/元 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 18 | 10 | 8 | 2 |
A.平均数为![]() 元B.众数为
元B.众数为![]() 元C.中位数为
元C.中位数为![]() 元D.极差为
元D.极差为![]() 元
元